题目内容
11.平面内的两条直线有相交和平行两种位置关系.(1)AB∥CD,如图(1)点P在AB、CD内部时,∠P=∠B+∠D.如图(2)点P在AB、CD外部时,以上结论是否成立?如不成立,则∠P、∠B、∠D之间有何数量关系?请说明理由.
(2)将如(1)中直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图(3),则∠BPD、∠B、∠D、∠BQD之间有何数量关系?请说明理由.

分析 (1)由AB∥CD,根据平行线的性质,易得∠BOD=∠B,又由三角形外角的性质可得:∠BOD=∠D+∠BPD,即可得出结论;
(2)连接QP,并延长交BD于E,由三角形的外角性质得出∠BPE=∠ABP+∠BQP,∠DPE=∠PDC+∠DQP,即可得出结论.
解答 解:(1)不成立.∠BPD=∠B-∠D.理由如下:
∵AB∥CD,
∴∠BOD=∠B,
∵∠BOD=∠BPD+∠D,
∴∠BPD=∠B-∠D;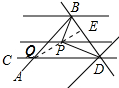
(2)∠BPD=∠ABP+∠PDC+∠BQD.理由如下:
连接QP,并延长交BD于E,如图所示:
∵∠BPE=∠ABP+∠BQP,∠DPE=∠PDC+∠DQP,
∴∠BPD=∠BPE+∠DPE=∠BQP+∠ABP+∠DQP+∠PDC=∠ABP+∠PDC+∠BQD.
点评 此题考查了平行线的性质以及三角形外角的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
1.已知点A(0,4),B点在x轴上,AB与坐标轴围成的三角形面积为2,则B点坐标是( )
| A. | (1,0)或(-1,0) | B. | (1,0) | C. | (0,1)或(0,-1) | D. | (-1,0) |
2.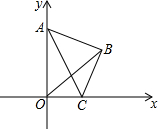 如图,在平面直角坐标系中,已知AB=BC,∠ABC=90°,若点A落在y轴上,点C落在x轴上,△ABC的形状始终不变,随着点C由原点O向x轴正半轴方向运动,点A沿y轴负半轴方向运动到终点O,在此次运动过程中,线段OB的长度变化情况是( )
如图,在平面直角坐标系中,已知AB=BC,∠ABC=90°,若点A落在y轴上,点C落在x轴上,△ABC的形状始终不变,随着点C由原点O向x轴正半轴方向运动,点A沿y轴负半轴方向运动到终点O,在此次运动过程中,线段OB的长度变化情况是( )
 如图,在平面直角坐标系中,已知AB=BC,∠ABC=90°,若点A落在y轴上,点C落在x轴上,△ABC的形状始终不变,随着点C由原点O向x轴正半轴方向运动,点A沿y轴负半轴方向运动到终点O,在此次运动过程中,线段OB的长度变化情况是( )
如图,在平面直角坐标系中,已知AB=BC,∠ABC=90°,若点A落在y轴上,点C落在x轴上,△ABC的形状始终不变,随着点C由原点O向x轴正半轴方向运动,点A沿y轴负半轴方向运动到终点O,在此次运动过程中,线段OB的长度变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减小 |
19.某同学使用计算器求30个数据的平均数时,错将其中的一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
| A. | -3.5 | B. | 3 | C. | 0.5 | D. | -3 |
6. 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,点P是线段AB上的一动点,将△ABC绕点C按顺时针方向旋转,得到△A1B1C1,点E是线段A1C的中点,则PE长度的最小值为( )
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,点P是线段AB上的一动点,将△ABC绕点C按顺时针方向旋转,得到△A1B1C1,点E是线段A1C的中点,则PE长度的最小值为( )
 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,点P是线段AB上的一动点,将△ABC绕点C按顺时针方向旋转,得到△A1B1C1,点E是线段A1C的中点,则PE长度的最小值为( )
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,点P是线段AB上的一动点,将△ABC绕点C按顺时针方向旋转,得到△A1B1C1,点E是线段A1C的中点,则PE长度的最小值为( )| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-1 | C. | $\sqrt{2}$+1 | D. | $\sqrt{3}$+1 |
16.适合下列条件的△ABC中,直角三角形的个数为( )
①a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$;
②a=6,∠A=45°;
③∠A=32°,∠B=58°;
④a=7,b=24,c=25.
①a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$;
②a=6,∠A=45°;
③∠A=32°,∠B=58°;
④a=7,b=24,c=25.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1.若x是2的相反数,|y|=3,则x-y的值是( )
| A. | -5 | B. | 1 | C. | -1 或 5 | D. | 1 或-5 |



