题目内容
16.适合下列条件的△ABC中,直角三角形的个数为( )①a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$;
②a=6,∠A=45°;
③∠A=32°,∠B=58°;
④a=7,b=24,c=25.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形;三角形内角和为180°进行分析即可.
解答 解:①($\frac{1}{5}$)2+($\frac{1}{4}$)2≠($\frac{1}{3}$)2,不能构成直角三角形;
②a=6,∠A=45°,不一定是直角三角形;
③∠A=32°,∠B=58°,则∠C=180°-32°-58°=90°,是直角三角形;
④72+242=252,能构成直角三角形;
能构成直角三角形的个数为2个,
故选:A.
点评 此题主要考查了直角三角形的判定,关键是掌握勾股定理的逆定理.

练习册系列答案
相关题目
1.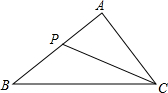 如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件,错误的是( )
如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件,错误的是( )
 如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件,错误的是( )
如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件,错误的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AP}{AC}$=$\frac{AC}{AB}$ | D. | $\frac{AC}{CP}$=$\frac{AB}{BC}$ |
8.若分式$\frac{3x}{x+1}$有意义,则x满足的条件是( )
| A. | x=-1 | B. | x≠-1 | C. | x=0 | D. | x≠0 |
5. △ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,则下列说法错误的是( )
△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,则下列说法错误的是( )
 △ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,则下列说法错误的是( )
△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,则下列说法错误的是( )| A. | 四边形ABED是矩形 | B. | AD${\;}_{=}^{∥}$CF | ||
| C. | BC=CF | D. | DF=CF |
6.若a2+b+5=0,则代数式3a2+3b+10的值为( )
| A. | 25 | B. | 5 | C. | -5 | D. | 0 |

 如果小球在如图所示的七巧板上自由滚动,并随机停留在这七巧板的某个位置上(不考虑停在边线的情况),那么它最终停留在四边形EFLH的概率是$\frac{1}{8}$.
如果小球在如图所示的七巧板上自由滚动,并随机停留在这七巧板的某个位置上(不考虑停在边线的情况),那么它最终停留在四边形EFLH的概率是$\frac{1}{8}$.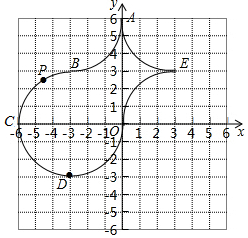 如图,在平面直角坐标系xOy中,几段$\frac{1}{4}$圆弧(占圆周的$\frac{1}{4}$的圆弧)首尾连接围成的封闭区域形如“宝瓶”,其中圆弧连接点都在正方形网格的格点处,点A的坐标是A(0,6),点C的坐标是C(-6,0).
如图,在平面直角坐标系xOy中,几段$\frac{1}{4}$圆弧(占圆周的$\frac{1}{4}$的圆弧)首尾连接围成的封闭区域形如“宝瓶”,其中圆弧连接点都在正方形网格的格点处,点A的坐标是A(0,6),点C的坐标是C(-6,0).