题目内容
10.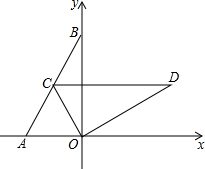 已知如图,在直角坐标系xOy中,点A,点B坐标分别为(-1,0),(0,$\sqrt{3}$),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
已知如图,在直角坐标系xOy中,点A,点B坐标分别为(-1,0),(0,$\sqrt{3}$),连结AB,OD由△AOB绕O点顺时针旋转60°而得.(1)求点C的坐标;
(2)△AOB绕点O顺时针旋转60°所扫过的面积;
(3)线段AB绕点O顺时针旋转60°所扫过的面积.
分析 (1)如图1,过C作CE⊥OA于E,由点A,点B坐标分别为(-1,0),(0,$\sqrt{3}$),得到OA=1,OB=$\sqrt{3}$,根据旋转的性质得到∠AOC=∠BOD=60°,AO=OC=1,解直角三角形即可得到结论;
(2)根据三角形和扇形的面积公式即可得到结论;
(3)根据三角形和扇形的面积公式即可得到结论;
解答 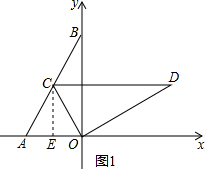 解:(1)如图1,过C作CE⊥OA于E,
解:(1)如图1,过C作CE⊥OA于E,
∵点A,点B坐标分别为(-1,0),(0,$\sqrt{3}$),
∴OA=1,OB=$\sqrt{3}$,
∵△AOB绕点O顺时针旋转60°得到△COD,
∴∠AOC=∠BOD=60°,AO=OC=1,
∴OE=$\frac{1}{2}$OC=$\frac{1}{2}$,CE=$\frac{\sqrt{3}}{2}$OC=$\frac{\sqrt{3}}{2}$,
∴C(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$);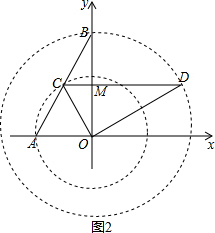
(2)△AOB绕点O顺时针旋转60°所扫过的面积=$\frac{60π•{1}^{2}}{360}$+$\frac{60π•(\sqrt{3})^{2}}{360}$+$\frac{1}{2}$×$\frac{1}{2}×\sqrt{3}$=$\frac{2}{3}$π+$\frac{\sqrt{3}}{4}$;
(3)如图2,线段AB绕点O顺时针旋转60°所扫过的面积═($\frac{60π•{1}^{2}}{360}$-1×$\frac{\sqrt{3}}{2}×\frac{1}{2}$)+($\frac{3}{2}×\frac{\sqrt{3}}{2}×\frac{1}{2}$-$\frac{60•π×(\frac{\sqrt{3}}{2})^{2}}{360}$)+($\frac{60•π×(\sqrt{3})^{2}}{360}$-$\frac{1}{2}×\frac{\sqrt{3}}{2}×\frac{3}{2}$)=$\frac{13}{24}$π+$\frac{\sqrt{3}}{4}$.
点评 此题考查了作图-旋转变换及扇形面积的计算,熟记扇形的面积公式是解题的关键.

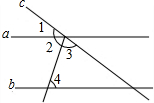 如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )
如图,直线a,b被直线c所截,a∥b,若∠2=∠3,∠4=63°,则∠1等于( )| A. | 54° | B. | 58° | C. | 63° | D. | 68° |
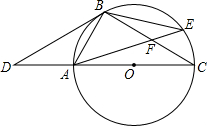 如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD. 如图,已知抛物线y=ax2+bx+c与x轴的两个交点A、B坐标分别为(-1,0),(-3,0),抛物线与y轴交点C为(0,3).
如图,已知抛物线y=ax2+bx+c与x轴的两个交点A、B坐标分别为(-1,0),(-3,0),抛物线与y轴交点C为(0,3).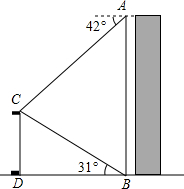 如图,某校数学兴趣小组在楼AB的顶部A处测得该楼正前方旗杆CD的顶端C的俯角为42°,在楼AB的底部B处测得旗杆CD的顶端C的仰角为31°,已知旗杆CD的高度为12m,根据测得的数据,计算楼AB的高度(结果保留整数).
如图,某校数学兴趣小组在楼AB的顶部A处测得该楼正前方旗杆CD的顶端C的俯角为42°,在楼AB的底部B处测得旗杆CD的顶端C的仰角为31°,已知旗杆CD的高度为12m,根据测得的数据,计算楼AB的高度(结果保留整数).