题目内容
5.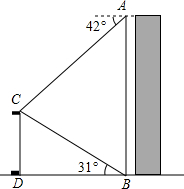 如图,某校数学兴趣小组在楼AB的顶部A处测得该楼正前方旗杆CD的顶端C的俯角为42°,在楼AB的底部B处测得旗杆CD的顶端C的仰角为31°,已知旗杆CD的高度为12m,根据测得的数据,计算楼AB的高度(结果保留整数).
如图,某校数学兴趣小组在楼AB的顶部A处测得该楼正前方旗杆CD的顶端C的俯角为42°,在楼AB的底部B处测得旗杆CD的顶端C的仰角为31°,已知旗杆CD的高度为12m,根据测得的数据,计算楼AB的高度(结果保留整数).参考数据:tan42°≈0.90,tan48°≈1.11,tan31°≈0.60.
分析 首先分析图形:根据题意构造直角三角形.本题涉及到两个直角三角形△AEC、△CBD,通过解这两个直角三角形求得AE、DC的长度,进而可解即可求出答案.
解答 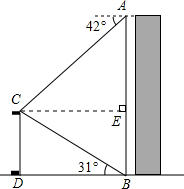 解:如图,过点C作CE⊥AB于点E.
解:如图,过点C作CE⊥AB于点E.
依题意得:∠ACE=42°,∠CBD=31°,CD=12m.
可得四边形CDBE是矩形.
∴BE=DC,CE=DB.
∵在直角△CBD中,tan∠CBD=$\frac{CD}{DB}$,
∴CE=DB=$\frac{CD}{tan31°}$.
∵在直角△ACE中,tan∠ACE=$\frac{AE}{CE}$.
∴AE=CE•tan42°.
∴AE=$\frac{CD}{tan31°}$•tan42°≈$\frac{12×0.90}{1.60}$=18(米).
∴AB=AE+BE=30(米).
答:楼AB的高度约为30米.
点评 本题考查解直角三角形的应用-仰角俯角问题.解直角梯形可以通过作高线转化为解直角三角形和矩形的问题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
15.自成都地铁4号线开通以来,成都地铁1、2、4号线线网客流增加明显,再遇到春季糖酒会、桃花节、通勤客流等三股主要客流汇集,2016年3月25日,成都地铁再创单日线网客流历史新高,达到1738200乘次,用科学记数法表示1738200为(保留三个有效数字)( )
| A. | 1.74×106 | B. | 1.73×106 | C. | 17.4×105 | D. | 17.3×105 |
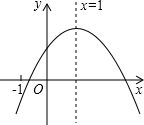 二次函数图象如图所示,对称轴为x=1,给出下列结论:
二次函数图象如图所示,对称轴为x=1,给出下列结论:
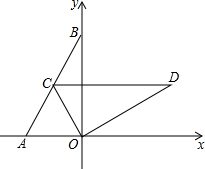 已知如图,在直角坐标系xOy中,点A,点B坐标分别为(-1,0),(0,$\sqrt{3}$),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
已知如图,在直角坐标系xOy中,点A,点B坐标分别为(-1,0),(0,$\sqrt{3}$),连结AB,OD由△AOB绕O点顺时针旋转60°而得.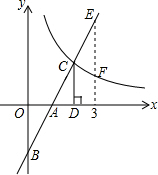 如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点D作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点D作CD⊥x轴,垂足为D,且OA=AD,则以下结论:



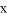 轴分别相交于点
轴分别相交于点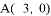 和点
和点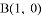 ,与
,与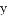 轴相交于
轴相交于 ,顶点为点
,顶点为点 。
。 的代数式表示);
的代数式表示);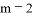 时,点
时,点 为第三象限内抛物线上的一个动点,设
为第三象限内抛物线上的一个动点,设 的面积为
的面积为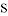 ,试求出
,试求出 、
、 三点为顶点的三角形与
三点为顶点的三角形与 相似?
相似?