题目内容
14.已知关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+1=0有两个实数根.(1)求k的取值范围;
(2)若抛物线y=x2-(k+1)x+$\frac{1}{4}$k2+1与x轴交于A、B两点,点A、点B到原点O的距离分别为OA、OB,且满足OA+OB-4OA•OB+5=0,求k的值.
分析 (1)由于关于x的一元二次方程x2-(2k+1)x+k2+2k=0有两个实数根,可知△≥0,据此进行计算即可;
(2)由根与系数的关系和已知条件得出关于k的方程,解方程即可.
解答 (1)解:∵原方程有两个实数根,
∴△=(k+1)2-4($\frac{1}{4}$k2+1)≥0
∴k2+2k+1-k2-4≥0,
解得:k≥$\frac{3}{2}$
(2)设A、B两点的坐标为A(x1,0)、B(x2,0)
则x1、x2是方程x2-(k+1)x+$\frac{1}{4}$k2+1=0的两根
∵$k≥\frac{3}{2}$,
∴x1+x2=k+1>0,x1•x2=$\frac{1}{4}$k2+1>0,
∴x1>0,x2>0,
∴OA+OB=|x1|+|x2|=x1+x2=k+1
OA•OB=|x1||x2|=4x1x2-5
∴k+1=4($\frac{1}{4}$k2+1)-5,
∴k2-k+2=0,
∴k1=-1,k2=2,
又∵k$≥\frac{3}{2}$,
∴k=2
点评 本题考查了根的判别式、根与系数的关系、抛物线与x轴的交点、一元二次方程的解法等知识;由根与系数的关系和已知条件得出关于k的方程是解决问题(2)的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.对于函数y=-2x+1,下列结论正确的是( )
| A. | 它的图象必经过点(-1,2) | B. | 它的图象经过第一、二、三象限 | ||
| C. | 当x>1时,y<0 | D. | y的值随x值的增大而增大 |
9.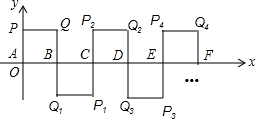 如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
 如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )| A. | (2016,1) | B. | (2015,1) | C. | (2016,-1) | D. | (4032,1) |
19.已知二次函数y=-x2+bx+c中,函数y与自变量x之间的部分对应值如表所示:
点A(x1,y1)、B(x2,y2)在函数的图象上,则当1<x1<2,3<x2<4时,则有( )
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | -1 | 2 | 3 | 2 | … |
| A. | y1>y2 | B. | y1<y2 | ||
| C. | y1=y2 | D. | y1与y2大小无法确定 |
4.已知A(x1,y1)、B(x2,y2)和C(x3,y3)在直线y=-$\frac{1}{2}$x+$\sqrt{3}$上.若x1<x2<x3,下列判断正确的是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3<y2<y1 |
 如图,在数轴上点A表示的实数是$\sqrt{5}$.
如图,在数轴上点A表示的实数是$\sqrt{5}$.