题目内容
11．一次函数y=-x+4的图象与两坐标轴所围成的三角形的面积为（ ）| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
分析 先求出直线与坐标轴的交点，再利用三角形的面积公式即可得出结论．
解答 解：∵令x=0，则y=4；令y=0，则x=4，
∴直线与两坐标轴的交点分别为：（0，4），（4，0），
∴一次函数y=-x+4的图象与两坐标轴所围成的三角形的面积=$\frac{1}{2}$×4×4=8．
故选D．
点评 本题考查的是一次函数图象上点的坐标特点，熟知坐标轴上点的坐标特点是解答此题的关键．
练习册系列答案
相关题目
1．某部队为了测量一批新制造的炮弹的杀伤半径，从中抽查了50枚炮弹，它们的杀伤半径（单位：千米）如表：
这批炮弹的平均杀伤半径是多少千米？
| 杀伤半径 | 20≤x＜40 | 40≤x＜60 | 60≤x＜80 | 80≤x＜100 |
| 数量 | 8 | 12 | 25 | 5 |
2．对于函数y=-2x+1，下列结论正确的是（ ）
| A． | 它的图象必经过点（-1，2） | B． | 它的图象经过第一、二、三象限 | ||
| C． | 当x＞1时，y＜0 | D． | y的值随x值的增大而增大 |
19．已知二次函数y=-x2+bx+c中，函数y与自变量x之间的部分对应值如表所示：
点A（x1，y1）、B（x2，y2）在函数的图象上，则当1＜x1＜2，3＜x2＜4时，则有（ ）
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | -1 | 2 | 3 | 2 | … |
| A． | y1＞y2 | B． | y1＜y2 | ||
| C． | y1=y2 | D． | y1与y2大小无法确定 |
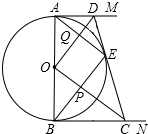如图所示，AB是⊙O的直径，AM、BN是⊙O的两条切线，D、C分别在AM、BN上，DC切⊙O于点E，连接OD、OC、BE、AE，BE与OC相交于点P，AE与OD相交于点Q，已知AD=4，BC=9，以下结论：