题目内容
6.解分式方程:(1)$\frac{x-1}{{x}^{2}+x}$+2=$\frac{2x}{x+1}$;
(2)$\frac{1}{x-1}$=$\frac{3}{{x}^{2}+x-2}$.
分析 (1)观察可得最简公分母是x(x+1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解;
(2)先把分母因式分解,再乘以最简公分母(x+2)(x-1),求出x的值,再进行检验即可得出答案.
解答 解:(1)$\frac{x-1}{{x}^{2}+x}$+2=$\frac{2x}{x+1}$,
$\frac{x+1}{x(x+1)}$+2=$\frac{2x}{x+1}$,
(x-1)+2x(x+1)=2x2,
x-1+2x2+2x=2x2,
3x=1,
x=$\frac{1}{3}$,
经检验x=$\frac{1}{3}$是原方程的解,
则原方程的解为:x=$\frac{1}{3}$;
(2)$\frac{1}{x-1}$=$\frac{3}{{x}^{2}+x-2}$,
$\frac{1}{x-1}$=$\frac{3}{(x+2)(x-1)}$,
方程的两边同乘(x+2)(x-1),得x+2=3,
解得:x=1,
检验:把x=1代入(x+2)(x-1)=0,
则原方程无解.
点评 本题考查解分式方程的能力,注意:解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解;解分式方程一定注意要验根.

练习册系列答案
相关题目
14.计算:
(1)(-x2y5)•(xy)3
(2)4a(a-b+1)
(3)10032(简便计算)
(4)x2-(x+1)(x-1)
(5)先化简再求值:(a-2)2+2(a-1)(a+2),其中a=-2.
(1)(-x2y5)•(xy)3
(2)4a(a-b+1)
(3)10032(简便计算)
(4)x2-(x+1)(x-1)
(5)先化简再求值:(a-2)2+2(a-1)(a+2),其中a=-2.
18.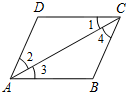 如图所示,下列推理及所注理由错误的是( )
如图所示,下列推理及所注理由错误的是( )
 如图所示,下列推理及所注理由错误的是( )
如图所示,下列推理及所注理由错误的是( )| A. | ∵∠1=∠3,∴AB∥CD(内错角相等,两直线平行) | |
| B. | ∵AB∥CD,∴∠1=∠3(两直线平行,内错角相等) | |
| C. | ∵AD∥BC,∴∠2=∠4(两直线平行,内错角相等) | |
| D. | ∵∠2=∠4,∴AB∥CD(内错角相等,两直线平行) |
15.下列说法错误的是( )
| A. | 必然事件的概率是1 | |
| B. | 如果某种游戏活动的中奖率为40%,那么参加这种活动10次必有4次中奖 | |
| C. | 了解一批灯泡的使用寿命适合用抽样调查 | |
| D. | 数据1、2、2、3的平均数是2 |
16. 如图,A,B,C,D为⊙O上的点,OC⊥AB于点E,若∠CDB=30°,OA=2,则AB的长为( )
如图,A,B,C,D为⊙O上的点,OC⊥AB于点E,若∠CDB=30°,OA=2,则AB的长为( )
 如图,A,B,C,D为⊙O上的点,OC⊥AB于点E,若∠CDB=30°,OA=2,则AB的长为( )
如图,A,B,C,D为⊙O上的点,OC⊥AB于点E,若∠CDB=30°,OA=2,则AB的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |
 如图∠1=75°,∠A=60°,∠B=45°
如图∠1=75°,∠A=60°,∠B=45°