题目内容
10.在学习“一次函数与二元一次方程”时,我们知道了两个一次函数图象的交点坐标与其相应的二元一次方程组的解之间的关系,请通过此经验推断:在同一平面直角坐标系中,函数y=5x2-3x+4与y=4x2-x+3的图象交点个数有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
分析 由题意知函数y=5x2-3x+4与y=4x2-x+3的图象交点个数即方程组$\left\{\begin{array}{l}{y=5{x}^{2}-3x+4}\\{y=4{x}^{2}-x+3}\end{array}\right.$的解的个数,即可判断.
解答 解:根据题意,函数y=5x2-3x+4与y=4x2-x+3的图象交点个数即方程组$\left\{\begin{array}{l}{y=5{x}^{2}-3x+4}\\{y=4{x}^{2}-x+3}\end{array}\right.$的解的个数,
解方程组得:$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$,
所以函数y=5x2-3x+4与y=4x2-x+3的图象交点只有一个交点(1,6),
故选:B.
点评 本题主要考查二次函数的性质,根据题意得出二次函数图象交点个数即为联立的方程组的解得个数是关键.

练习册系列答案
相关题目
1.在平面直角坐标系中,将点B(-3,2)向右平移5个单位长度,再向下平移3个单位长度后与点A(x,y)重合,则点A的坐标是( )
| A. | (2,5) | B. | (-8,5) | C. | (-8,-1) | D. | (2,-1) |
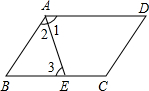 如图所示,在平行四边形ABCD中,∠BAD的平分线AE分对边长度为3和4两部分,求四边形ABCD的周长.
如图所示,在平行四边形ABCD中,∠BAD的平分线AE分对边长度为3和4两部分,求四边形ABCD的周长. 如图,AD=AE,请你添加一个条件AB=AC或∠ADC=∠AEB或∠ABE=∠ACD,使得△ADC≌△AEB.
如图,AD=AE,请你添加一个条件AB=AC或∠ADC=∠AEB或∠ABE=∠ACD,使得△ADC≌△AEB.



 以等腰△ABC的腰AB为直径作半圆,设圆心为点O,半圆与另一腰交于点D,与底BC交于点E,取线段CD的中点F,连接EF.
以等腰△ABC的腰AB为直径作半圆,设圆心为点O,半圆与另一腰交于点D,与底BC交于点E,取线段CD的中点F,连接EF.