题目内容
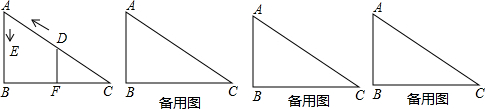
8.如图,△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°.点D从C出发沿CA以2个单位/s的速度向终点A运动,同时点E从A出发沿AB以1个单位/s的速度向终点B运动,DF⊥BC于F.设点D、E运动的时间是ts.(1)求证:AE=DF.
(2)连接EF,问:是否存在t,使四边形AEFD为菱形?若存在,求t的值;若不存在,请说明理由.
(3)连接DE、EF,当C为何值时,△DEF是直角三角形?为什么?
分析 (1)由“在直角三角形中,30度角所对的直角边是斜边的一半”求得DF=t,又AE=t,则DF=AE;
(2)而由垂直得到AB∥DF,即“四边形AEFD的对边平行且相等”,由此得四边形AEFD是平行四边形;
(3)①显然∠DFE<90°;
②如图①′,当∠EDF=90°时,四边形EBFD为矩形,此时 AE=$\frac{1}{2}$AD,根据题意,列出关于t的方程,通过解方程来求t的值;
③如图①″,当∠DEF=90°时,此时∠ADE=90°-∠A=30°,此时AD=$\frac{1}{2}$AE,根据题意,列出关于t的方程,通过解方程来求t的值.
解答 (1)证明:如图①,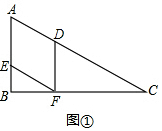
∵DF⊥BC,∠C=30°,
∴DF=$\frac{1}{2}$CD=$\frac{1}{2}$×2t=t.
∵AE=t,
∴DF=AE;
(2)解:存在t,使四边形AEFD为菱形,
理由是:∵在△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°,
∴AB=$\frac{5\sqrt{3}}{\sqrt{3}}$=5,AC=2AB=10,
∵∠ABC=90°,DF⊥BC,
∴DF∥AE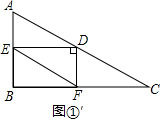 ,
,
∵AE=DF,
∴四边形AEFD是平行四边形,
∴当AE=AD时,四边形AEFD是菱形,
∵AE=t,DC=2t,
∴AD=t,
t+2t=10,
∴t=$\frac{10}{3}$,
即存在t,使四边形AEFD为菱形,此时t=$\frac{10}{3}$;
(3)解:①显然∠DFE<90°;
②如图①′,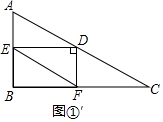
当∠EDF=90°时,四边形EBFD为矩形,
此时 AE=$\frac{1}{2}$AD,
∴t=$\frac{1}{2}$(10-2t),
解得:t=$\frac{5}{2}$;
③如图①″,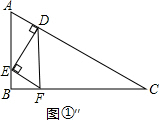
当∠DEF=90°时,此时∠ADE=90°
∴∠AED=90°-∠A=30°
∴AD=$\frac{1}{2}$AE,
∴10-2t=$\frac{1}{2}$t,
解得:t=4,
综上:当t=$\frac{5}{2}$秒或4秒时,△DEF为直角三角形;
点评 本题考查了四边形综合题,解题时,需要综合运用直角三角形的性质,菱形的性质以及平行四边形的判定与性质,另外,解题时,需要分类讨论.

| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 2 | D. | 4 |
| A. | 只有一个交点 | B. | 有两个交点 | C. | 没有交点 | D. | 不能确定 |

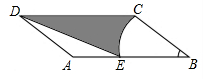 如图,在平行四边形ABCD中,AB=5,AD=2,∠B=60°,以点B为圆心,BG为半径的圆弧交AB于点E,连接DE,则图中阴影部分的面积为$\frac{7\sqrt{3}}{2}$-$\frac{2}{3}$π.(结果保留π)
如图,在平行四边形ABCD中,AB=5,AD=2,∠B=60°,以点B为圆心,BG为半径的圆弧交AB于点E,连接DE,则图中阴影部分的面积为$\frac{7\sqrt{3}}{2}$-$\frac{2}{3}$π.(结果保留π)