题目内容
20.一次函数y=kx+b的图象与正比例函数y=-3x的图象平行,并且与y轴的交点坐标为(0,4),则$\sqrt{-kb}$的值为2$\sqrt{3}$.分析 据两条直线相交或平行问题由一次函数y=kx+b的图象与正比例函数y=-3x的图象平行得到k=-3,然后把点(0,4)代入一次函数解析式可求出b的值,最后计算出$\sqrt{-kb}$即可.
解答 解:∵一次函数y=kx+b的图象与正比例函数y=-3x的图象平行,
∴k=-3,
∴y=-3x+b,
把点(0,4)代入y=-3x+b得b=4,
∴$\sqrt{-kb}$=$\sqrt{-(-3)×4}$=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题考查了两条直线相交或平行问题:若直线y=k1x+b1与直线y=k2x+b2平行,则k1=k2;若直线y=k1x+b1与直线y=k2x+b2相交,则由两解析式所组成的方程组的解为交点坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )
如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )
 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )
如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
15.计算(-3)×(-5)的结果是( )
| A. | 15 | B. | -15 | C. | 8 | D. | -8 |
 如图,已知菱形ABCD的周长为16cm,AE垂直平分BC,垂足为E
如图,已知菱形ABCD的周长为16cm,AE垂直平分BC,垂足为E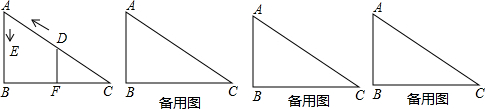
 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径.
如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径.