题目内容
3.把图1的矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图2),已知∠MPN=90°,PM=5,PN=12,求矩形纸片ABCD的面积.
分析 先在Rt△MPN中,利用勾股定理,求得MN=13,再根据折叠的性质,得出BC=5+13+12=30,然后由直角三角形的面积公式,得到AB=$\frac{60}{13}$,进而求得矩形的面积.
解答 解:∵∠MPN=90°,PM=5,PN=12,
∴MN=13,BC=5+13+12=30.
根据直角三角形的面积公式,得
AB=$\frac{PM•PN}{MN}$=$\frac{60}{13}$,
∴矩形的面积=30×$\frac{60}{13}$=$\frac{1800}{13}$.
故矩形ABCD的面积为$\frac{1800}{13}$.
点评 此题综合运用了勾股定理、折叠的性质和直角三角形的斜边上的高等于两直角边的乘积除以斜边的方法,本题难度适中.

练习册系列答案
相关题目
11. 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )
如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )
 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )
如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
15.计算(-3)×(-5)的结果是( )
| A. | 15 | B. | -15 | C. | 8 | D. | -8 |
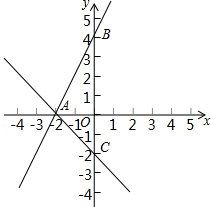 如图,一次函数y=2x+a与y=-x+b的图象都经过点A(-2,0),且与y轴分别交于B、C两点,则△ABC的面积为6.
如图,一次函数y=2x+a与y=-x+b的图象都经过点A(-2,0),且与y轴分别交于B、C两点,则△ABC的面积为6.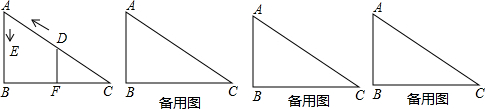
 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径.
如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径.