题目内容
16.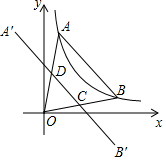 如图,点A、B在函数y=$\frac{1}{x}$(x>0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′分别交OA、OB于点D、C.若四边形ABCD的面积为$\frac{6}{5}$,则点A的坐标为($\frac{1}{2}$,2),点C的坐标为($\frac{6}{5}$,$\frac{3}{10}$).
如图,点A、B在函数y=$\frac{1}{x}$(x>0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′分别交OA、OB于点D、C.若四边形ABCD的面积为$\frac{6}{5}$,则点A的坐标为($\frac{1}{2}$,2),点C的坐标为($\frac{6}{5}$,$\frac{3}{10}$).
分析 因为反比例函数y=$\frac{1}{x}$,关于直线y=x对称,因为OA=OB,所以A、B关于直线y=x对称,可以设点A的坐标为(m,$\frac{1}{m}$),则点B的坐标为($\frac{1}{m}$,m),则点A′的坐标为(-m,$\frac{1}{m}$),点B′的坐标为($\frac{1}{m}$,-m),求出直线OB、A′B′的解析式,解方程组求出点C的坐标,求出线段CD、AB,列出方程求出m即可解决问题.
解答 解:∵反比例函数y=$\frac{1}{x}$,关于直线y=x对称,
∵OA=OB,
∴A、B关于直线y=x对称,
设点A的坐标为(m,$\frac{1}{m}$),则点B的坐标为($\frac{1}{m}$,m),则点A′的坐标为(-m,$\frac{1}{m}$),点B′的坐标为($\frac{1}{m}$,-m),
∴直线OB的解析式为y=m2x,
直线A′B′的解析式为y=-x+$\frac{1}{m}$-m,
由$\left\{\begin{array}{l}{y={m}^{2}x}\\{y=-x+\frac{1}{m}-m}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{1-{m}^{2}}{m({m}^{2}+1)}}\\{y=\frac{m(1-{m}^{2})}{{m}^{2}+1}}\end{array}\right.$,
∴C[$\frac{1-{m}^{2}}{m({m}^{2}+1)}$,$\frac{m(1-{m}^{2})}{{m}^{2}+1}$],根据对称性可知D[$\frac{m(1-{m}^{2})}{{m}^{2}+1}$,$\frac{1-{m}^{2}}{m({m}^{2}+1)}$],
如图,设A′B′交x轴于F,交y轴于E,连接AA′,作DN⊥OF于N,CM⊥OE于M,DN交CM于G.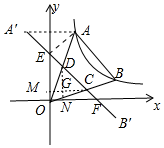
∵OE=OF=$\frac{1}{m}$-m,
∴∠OEF=∠OFE=45°,
∴∠A′EA=90°,AE=$\sqrt{2}$m,
在Rt△CDG中,∵DG=CG,CD=$\sqrt{2}$CG=$\sqrt{2}$[$\frac{1-{m}^{2}}{m({m}^{2}+1)}$-$\frac{m(1-{m}^{2})}{{m}^{2}+1}$].
同理可得,AB=$\sqrt{2}$($\frac{1}{m}$-m),
∵四边形ADCB的面积为$\frac{6}{5}$,
∴$\frac{\sqrt{2}(\frac{1}{m}-m)+\sqrt{2}[\frac{1-{m}^{2}}{m({m}^{2}+1)}-\frac{m(1-{m}^{2})}{{m}^{2}+1}]}{2}$•$\sqrt{2}$m=$\frac{6}{5}$,
整理得$\frac{2(1-{m}^{2})}{{m}^{2}+1}$=$\frac{6}{5}$,解得m2=$\frac{1}{4}$,∵m>0,
∴m=$\frac{1}{2}$,
∴A($\frac{1}{2}$,2),C($\frac{6}{5}$,$\frac{3}{10}$).
故答案为($\frac{1}{2}$,2)或($\frac{6}{5}$,$\frac{3}{10}$).
点评 本题考查反比例函数图象上点的特征、一次函数函数的应用、轴对称、等腰直角三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,学会构建一次函数,利用方程组确定直线的交点坐标,属于中考填空题中的压轴题.


 如图,A,B是直线l上的两点,AB=4厘米,过l外一点C作CD∥l,射线BC与l所组成的锐角为60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以1厘米/秒的速度,沿由B向C的方向运动;Q以2厘米/秒的速度,沿由C向D的方向运动,设P、Q运动的时间为t秒,当t>2时,PA交CD于点E.
如图,A,B是直线l上的两点,AB=4厘米,过l外一点C作CD∥l,射线BC与l所组成的锐角为60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以1厘米/秒的速度,沿由B向C的方向运动;Q以2厘米/秒的速度,沿由C向D的方向运动,设P、Q运动的时间为t秒,当t>2时,PA交CD于点E.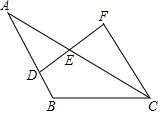 如图,已知AB∥CF,E为DF的中点,若AB=13cm,CF=9cm,则BD=4cm.
如图,已知AB∥CF,E为DF的中点,若AB=13cm,CF=9cm,则BD=4cm. 如图,从以下四个条件:①BC=EC; ②AC=DC;③∠DCA=∠ECB; ④AB=DE.
如图,从以下四个条件:①BC=EC; ②AC=DC;③∠DCA=∠ECB; ④AB=DE.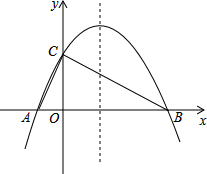 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0). 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5$\sqrt{5}$,则四边形ABCD的面积为=31,BD的长为2$\sqrt{41}$.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5$\sqrt{5}$,则四边形ABCD的面积为=31,BD的长为2$\sqrt{41}$.