题目内容
1. 定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{-3,2}=2.
定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{-3,2}=2.(1)max{$\sqrt{11}$,3}=$\sqrt{11}$;
(2)已知y1=$\frac{{k}_{1}}{x}$和y2=k2x+b在同一坐标系中的图象如图所示,若max{$\frac{{k}_{1}}{x}$,k2x+b}=$\frac{{k}_{1}}{x}$,结合图象,直接写出x的取值范围;
(3)试用分类讨论的方法,求max{x+2,x2-4}的值.
分析 (1)根据3$<\sqrt{11}$和已知求出即可;
(2)根据题意得出$\frac{{k}_{1}}{x}$≥k2x+b,结合图象求出即可;
(3)分为两种情况:当x+2≥x2-4,时,当x+2<x2-4,时,结合已知求出即可.
解答 解:(1)max{$\sqrt{11}$,3}=$\sqrt{11}$,
故答案为:$\sqrt{11}$;
(2)∵max{$\frac{{k}_{1}}{x}$,k2x+b}=$\frac{{k}_{1}}{x}$,
∴$\frac{{k}_{1}}{x}$≥k2x+b,
∴从图象可知:x的取值范围为-3≤x<0或x≥2;
(3)由图易知当-2≤x≤3时x+2≥x2-4,max{x+2,x2-4 }=x+2,
由图易知当当x<-2或x>3时,x+2<x2-4,max{x+2,x2-4 }=x2-4.
点评 本题考查了反比例函数和一次函数的交点问题,读懂题目信息,理解定义符号的意义并考虑求两个函数的交点是解题的关键.

练习册系列答案
相关题目
13.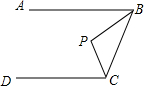 如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
 如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )| A. | 120° | B. | 90° | C. | 75° | D. | 60° |
 如图,在扇形AOB中,∠AOB=90°,弧AB的长为2π,则扇形AOB的面积为4π.
如图,在扇形AOB中,∠AOB=90°,弧AB的长为2π,则扇形AOB的面积为4π.