题目内容
10．
如图，在扇形AOB中，∠AOB=90°，弧AB的长为2π，则扇形AOB的面积为4π．
分析 首先运用弧长公式求出扇形的半径，运用扇形的面积公式直接计算，即可解决问题．
解答 解：∵∠AOB=90°，弧AB的长为2π，
∴$\frac{90πr}{180}$=2π，
解得：r=4，
∴扇形的面积为$\frac{90π×{4}^{2}}{360}$=4π．
故答案为：4π．
点评 此题主要考查了扇形的面积公式、弧长公式等知识点及其应用问题；应牢固掌握扇形的面积公式、弧长公式，这是灵活运用、解题的基础和关键．
练习册系列答案
名校课堂系列答案
相关题目
20．已知点A（a，-3），B（4，b）关于y轴的对称，则a+b的值为（ ）
| A． | 1 | B． | 7 | C． | -7 | D． | -1 |
定义运算max{a，b}：当a≥b时，max{a，b}=a；当a＜b时，max{a，b}=b．如max{-3，2}=2．
18．下列说法中，正确的是（ ）
| A． | 若ac=bc，则a=b | B． | 若$\frac{a}{c}$=$\frac{b}{c}$，则a=b | C． | 若a2=b2，则a=b | D． | 若|a|=|b|，则a=b |
5．一元二次方程x2=x的解为（ ）
| A． | x=1 | B． | x=0 | C． | x1=1，x2=2 | D． | x1=0，x2=1 |
2．下列说法正确的是（ ）
| A． | 棱柱的侧面可以是正方形，也可以是三角形 | |
| B． | 一个几何体的表面不可能只有曲面组成 | |
| C． | 棱柱的各条棱都相等 | |
| D． | 圆锥是由平面和曲面组成的几何体 |
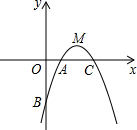已知二次函数y=-x2+4x-3，其图象与y轴交于点B，与x轴交于A、C 两点，顶点为M．