题目内容
13.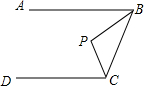 如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )| A. | 120° | B. | 90° | C. | 75° | D. | 60° |
分析 根据到角的两边距离相等的点在角的平分线上可得BP、CP分别是∠ABC和∠BCD的平分线,再根据两直线平行,同旁内角互补和角平分线的定义解答即可.
解答 解:∵点P到AB、BC、CD距离都相等,
∴BP、CP分别是∠ABC和∠BCD的平分线,
∴∠CBP=$\frac{1}{2}$∠ABC,∠BCP=$\frac{1}{2}$∠BCD,
∴∠CBP+∠BCP=$\frac{1}{2}$(∠ABC+∠BCD),
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠CBP+∠BCP=$\frac{1}{2}$×180°=90°,
∴∠P=180°-(∠CBP+∠BCP)=180°-90°=90°.
故选B.
点评 本题考查了角平分线的性质,平行线的性质,角平分线的定义,是基础题,熟记性质是解题的关键.

练习册系列答案
相关题目
18.下列说法中,正确的是( )
| A. | 若ac=bc,则a=b | B. | 若$\frac{a}{c}$=$\frac{b}{c}$,则a=b | C. | 若a2=b2,则a=b | D. | 若|a|=|b|,则a=b |
5.一元二次方程x2=x的解为( )
| A. | x=1 | B. | x=0 | C. | x1=1,x2=2 | D. | x1=0,x2=1 |
2.下列说法正确的是( )
| A. | 棱柱的侧面可以是正方形,也可以是三角形 | |
| B. | 一个几何体的表面不可能只有曲面组成 | |
| C. | 棱柱的各条棱都相等 | |
| D. | 圆锥是由平面和曲面组成的几何体 |
 定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{-3,2}=2.
定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{-3,2}=2.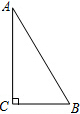 如图,在Rt△ABC中,∠C=90°,∠A=30°.
如图,在Rt△ABC中,∠C=90°,∠A=30°.