题目内容
3．
如图，每个小正方形的边长都相等，A、B、C是小正方形的顶点，则∠ABC的度数为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 根据勾股定理即可得到AB，BC，AC的长度，进行判断即可．
解答 解：连接AC，设每个小正方形的边长都是a，
根据勾股定理可以得到：AC=BC=$\sqrt{5}$a，AB=$\sqrt{10}$a，
∵（$\sqrt{5}$a）2+（$\sqrt{5}$a）2=（$\sqrt{10}$a）2，
∴AC2+BC2=AB2，
∴△ABC是等腰直角三角形，
∴∠ABC=45°，
故选B．
点评 本题主要考查了勾股定理，利用勾股定理判断△ABC是等腰直角三角形是解决本题的关键．
练习册系列答案
相关题目
14．下列运算正确的是（ ）
| A． | x2+x3=x6 | B． | （x3）2=x6 | C． | 2x+3y=5xy | D． | x6÷x3=x2 |
14．
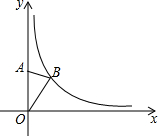如图，在平面直角坐标系中，点A是y轴正半轴上的一个定点，点B是反比例函数y=$\frac{k}{x}$（k为常数）在第一象限内图象上的一个动点．当点B的纵坐标逐渐增大时，△OAB的面积（ ）
如图，在平面直角坐标系中，点A是y轴正半轴上的一个定点，点B是反比例函数y=$\frac{k}{x}$（k为常数）在第一象限内图象上的一个动点．当点B的纵坐标逐渐增大时，△OAB的面积（ ）| A． | 逐渐减小 | B． | 逐渐增大 | C． | 先增大后减小 | D． | 不变 |
11．
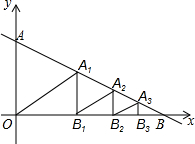如图，已知直线y=-$\frac{1}{2}$x+2与x轴交于点B，与y轴交于点A．过线段AB的中点A1做A1B1⊥x轴于点B1，过线段A1B的中点A2作A2B2⊥x轴于点B2，过线段A2B的中点A3作A3B3⊥x轴于点B3…，以此类推，则△AnBnBn-1的面积为（ ）
如图，已知直线y=-$\frac{1}{2}$x+2与x轴交于点B，与y轴交于点A．过线段AB的中点A1做A1B1⊥x轴于点B1，过线段A1B的中点A2作A2B2⊥x轴于点B2，过线段A2B的中点A3作A3B3⊥x轴于点B3…，以此类推，则△AnBnBn-1的面积为（ ）| A． | $\frac{1}{{2}^{n-1}}$ | B． | $\frac{1}{{2}^{n}}$ | C． | $\frac{1}{{4}^{n-1}}$ | D． | $\frac{1}{{4}^{n}}$ |
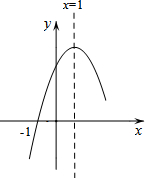如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，且对称轴为直线x=1，点B坐标为（-1，0）．则下面的四个结论：①2a+b=0；②8a+c＜0；③abc＞0；④当y＜0时，x＜-1或x＞2，⑤对任意实数m，m（am+b）≤a+b．其中正确的结论有（ ）个．
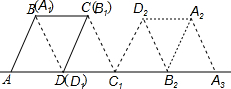如图，在菱形ABCD中，AB=4cm，∠BAD=60°，将菱形ABCD绕点D按顺时针方向作第一次旋转得到菱形A1B1C1D1，使点C落在点C1的位置，再将其绕点C1按顺时针方向作第二次旋转，使点B1落在点B2的位置…如此旋转下去，当点A2落在A3的位置时，点A在旋转过程中经过的路径长为$\frac{8+8\sqrt{3}}{3}$cm．