题目内容
14.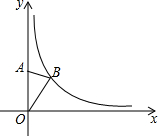 如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )| A. | 逐渐减小 | B. | 逐渐增大 | C. | 先增大后减小 | D. | 不变 |
分析 先根据函数图象判断出函数的增减性,再由三角形的面积公式即可得出结论.
解答 解:∵反比例函数y=$\frac{k}{x}$(k为常数)的图象在第一象限,
∴y随x的增大而减小.
∵点A是y轴正半轴上的一个定点,
∴OA是定值.
∵点B的纵坐标逐渐增大,
∴其横坐标逐渐减小,即△OAB的底边OA一定,高逐渐减小,
∴△OAB的面积逐渐减小.
故选A.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.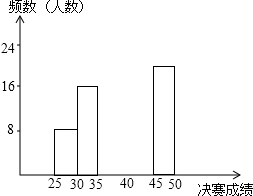 为增强学生的环保意识,某校组织学生开展了“雾霾天气知多少宣传暨竞赛活动”,经各班选拔,共推选出100名学会说呢过参加本次竞赛的决赛活动,决赛题设置了50道选择题,每答对一题得1分,满分50分,学校竞赛组委会经过统计,把这100名参赛学生的决赛成绩分成了5个组,并绘制出部分频数分布表和部分频数分布直方图如下:
为增强学生的环保意识,某校组织学生开展了“雾霾天气知多少宣传暨竞赛活动”,经各班选拔,共推选出100名学会说呢过参加本次竞赛的决赛活动,决赛题设置了50道选择题,每答对一题得1分,满分50分,学校竞赛组委会经过统计,把这100名参赛学生的决赛成绩分成了5个组,并绘制出部分频数分布表和部分频数分布直方图如下:
请结合图完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第1组8名同学中,有4名男同学,现将这8名同学平均分成两组参加学校环保宣传活动,4名男同学每组分2人,求小宇与小强两名男同学能分在同一组的概率.
 为增强学生的环保意识,某校组织学生开展了“雾霾天气知多少宣传暨竞赛活动”,经各班选拔,共推选出100名学会说呢过参加本次竞赛的决赛活动,决赛题设置了50道选择题,每答对一题得1分,满分50分,学校竞赛组委会经过统计,把这100名参赛学生的决赛成绩分成了5个组,并绘制出部分频数分布表和部分频数分布直方图如下:
为增强学生的环保意识,某校组织学生开展了“雾霾天气知多少宣传暨竞赛活动”,经各班选拔,共推选出100名学会说呢过参加本次竞赛的决赛活动,决赛题设置了50道选择题,每答对一题得1分,满分50分,学校竞赛组委会经过统计,把这100名参赛学生的决赛成绩分成了5个组,并绘制出部分频数分布表和部分频数分布直方图如下:| 组别 | 决赛成绩 x(分) | 频数(人数) |
| 第1组 | 25≤x<30 | 8 |
| 第2组 | 30≤x<35 | 16 |
| 第3组 | 35≤x<40 | 32 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 20 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第1组8名同学中,有4名男同学,现将这8名同学平均分成两组参加学校环保宣传活动,4名男同学每组分2人,求小宇与小强两名男同学能分在同一组的概率.
9.下列说法正确的是( )
| A. | 若两条直线被第三条直线所截,则同旁内角互补 | |
| B. | 点到直线的距离是指直线外一点到这条直线的垂线段 | |
| C. | $\sqrt{81}$的算术平方根是9 | |
| D. | 同一平面内,若直线a∥b,a⊥c,则b⊥c |
19.下列等式从左到右的变形,属于因式分解的是( )
| A. | (x+3)(x-3)=x2-9 | B. | x2-4+3x=(x+2)(x-2)+3x | ||
| C. | (x-1)2=x2-2x+1 | D. | xy2-x2y=xy(y-x) |
6.一个不透明的袋子中只装有4个红球,从中随机摸出一个球是红球( )
| A. | 属于随机事件 | B. | 可能性大小为$\frac{1}{4}$ | C. | 属于不可能事件 | D. | 是必然事件 |
3. 如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )
如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )
 如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )
如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
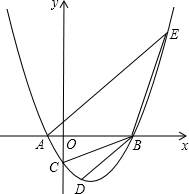 设抛物线y=ax2+bx-2与x轴交于两个不同的点A(一1,0)、B(4,0),与y轴交于点C.
设抛物线y=ax2+bx-2与x轴交于两个不同的点A(一1,0)、B(4,0),与y轴交于点C.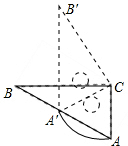 如图,Rt△ABC中,∠B=30°,斜边AB长12为cm,绕直角顶点C顺时针旋转,当点A落在AB边上的A′处,则弧AA′的长为2π cm.(结果保留π)
如图,Rt△ABC中,∠B=30°,斜边AB长12为cm,绕直角顶点C顺时针旋转,当点A落在AB边上的A′处,则弧AA′的长为2π cm.(结果保留π) 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,点A为⊙O上一动点,弦AB过点P,则AB最长为6,AB最短为2$\sqrt{6}$.
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,点A为⊙O上一动点,弦AB过点P,则AB最长为6,AB最短为2$\sqrt{6}$.