题目内容
8.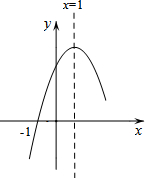 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②8a+c<0;③abc>0;④当y<0时,x<-1或x>2,⑤对任意实数m,m(am+b)≤a+b.其中正确的结论有( )个.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②8a+c<0;③abc>0;④当y<0时,x<-1或x>2,⑤对任意实数m,m(am+b)≤a+b.其中正确的结论有( )个.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据抛物线开口方向、对称轴、抛物线与y轴的交点确定a、b、c的符号,根据函数图象确定y>0和y<0时,x的取值范围.
解答 解:①对称轴-$\frac{b}{2a}$=1,∴2a+b=0,①正确;
②x=-2时,y<0,
∴4a-2b+c<0,由b=-2a,
∴8a+c<0,②正确;
③开口向下,a<0,
对称轴在y轴右侧,b>0,
与y轴交于正半轴,c>0,
∴abc<0,③错误;
④当x<-1或x>3时,y<0,④错误;
⑤当x=1时,函数有最大值,
∴am2+bm+c≤a+b+c,
∴m(am+b)≤a+b,⑤正确.
故选:B.
点评 本题考查的是二次函数的图象与系数的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
相关题目
19.下列等式从左到右的变形,属于因式分解的是( )
| A. | (x+3)(x-3)=x2-9 | B. | x2-4+3x=(x+2)(x-2)+3x | ||
| C. | (x-1)2=x2-2x+1 | D. | xy2-x2y=xy(y-x) |
16. 如图,该几何体的俯视图是( )
如图,该几何体的俯视图是( )
 如图,该几何体的俯视图是( )
如图,该几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
3. 如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )
如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )
 如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )
如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
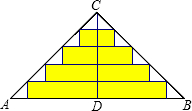 如图,△ABC是一张直角三角形彩色纸,AC=15cm,BC=20cm.若将斜边上的高CD 分成n等分,然后裁出(n-1)张宽度相等的长方形纸条.则这(n-1)张纸条的面积和是$\frac{150(n-1)}{n}$cm2.
如图,△ABC是一张直角三角形彩色纸,AC=15cm,BC=20cm.若将斜边上的高CD 分成n等分,然后裁出(n-1)张宽度相等的长方形纸条.则这(n-1)张纸条的面积和是$\frac{150(n-1)}{n}$cm2.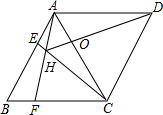 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( )