题目内容
11.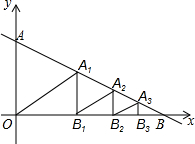 如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点A.过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,以此类推,则△AnBnBn-1的面积为( )
如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点A.过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,以此类推,则△AnBnBn-1的面积为( )| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{1}{{4}^{n-1}}$ | D. | $\frac{1}{{4}^{n}}$ |
分析 根据题意得出OB1=BB1=$\frac{1}{2}$OB,A1B1=$\frac{1}{2}$OA,B1B2=$\frac{1}{2}$BB1=$\frac{1}{4}$OB,A2B2=$\frac{1}{2}$A1B1=$\frac{1}{4}$OA,…,进而根据三角形面积得出S${\;}_{△{A}_{1}{B}_{1}O}$=$\frac{1}{2}$OB1•A1B1=$\frac{1}{2}$×$\frac{1}{2}$OB•$\frac{1}{2}$OA=$\frac{1}{4}$S△AOB=1
S${\;}_{△{A}_{2}{B}_{2}{B}_{1}}$=$\frac{1}{4}$S${\;}_{△{A}_{1}{B}_{1}O}$=$\frac{1}{4}$,S${\;}_{△{A}_{3}{B}^{3}{B}_{2}}$=$\frac{1}{4}$S${\;}_{△{A}_{2}{B}_{2}{B}_{1}}$=$\frac{1}{16}$,…,得出规律从而求得S△AnBnBn-1=$\frac{1}{{4}^{n-1}}$.
解答 解:∵直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点A.
∴A(0,2),B(4,0),
∴OA=2,OB=4,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×2×4=4,
∵过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,
∴OB1=BB1=$\frac{1}{2}$OB,A1B1=$\frac{1}{2}$OA,B1B2=$\frac{1}{2}$BB1=$\frac{1}{4}$OB,A2B2=$\frac{1}{2}$A1B1=$\frac{1}{4}$OA,…,
∴S${\;}_{△{A}_{1}{B}_{1}O}$=$\frac{1}{2}$OB1•A1B1=$\frac{1}{2}$×$\frac{1}{2}$OB•$\frac{1}{2}$OA=$\frac{1}{4}$S△AOB=1,
S${\;}_{△{A}_{2}{B}_{2}{B}_{1}}$=$\frac{1}{4}$S${\;}_{△{A}_{1}{B}_{1}O}$=$\frac{1}{4}$,
S${\;}_{△{A}_{3}{B}^{3}{B}_{2}}$=$\frac{1}{4}$S${\;}_{△{A}_{2}{B}_{2}{B}_{1}}$=$\frac{1}{16}$,
…,
∴S△AnBnBn-1=$\frac{1}{{4}^{n-1}}$.
故选C.
点评 本题考查了一次函数图象上点的坐标特征以及三角形面积的比等于相似比的平方;解此题的关键是根据求出的结果得出规律,题型较好,但是有一定的难度.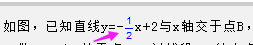

 名校课堂系列答案
名校课堂系列答案| A. | (x+3)(x-3)=x2-9 | B. | x2-4+3x=(x+2)(x-2)+3x | ||
| C. | (x-1)2=x2-2x+1 | D. | xy2-x2y=xy(y-x) |
| A. | 属于随机事件 | B. | 可能性大小为$\frac{1}{4}$ | C. | 属于不可能事件 | D. | 是必然事件 |
 如图,该几何体的俯视图是( )
如图,该几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )
如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
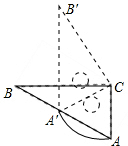 如图,Rt△ABC中,∠B=30°,斜边AB长12为cm,绕直角顶点C顺时针旋转,当点A落在AB边上的A′处,则弧AA′的长为2π cm.(结果保留π)
如图,Rt△ABC中,∠B=30°,斜边AB长12为cm,绕直角顶点C顺时针旋转,当点A落在AB边上的A′处,则弧AA′的长为2π cm.(结果保留π)