题目内容
11.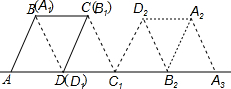 如图,在菱形ABCD中,AB=4cm,∠BAD=60°,将菱形ABCD绕点D按顺时针方向作第一次旋转得到菱形A1B1C1D1,使点C落在点C1的位置,再将其绕点C1按顺时针方向作第二次旋转,使点B1落在点B2的位置…如此旋转下去,当点A2落在A3的位置时,点A在旋转过程中经过的路径长为$\frac{8+8\sqrt{3}}{3}$cm.
如图,在菱形ABCD中,AB=4cm,∠BAD=60°,将菱形ABCD绕点D按顺时针方向作第一次旋转得到菱形A1B1C1D1,使点C落在点C1的位置,再将其绕点C1按顺时针方向作第二次旋转,使点B1落在点B2的位置…如此旋转下去,当点A2落在A3的位置时,点A在旋转过程中经过的路径长为$\frac{8+8\sqrt{3}}{3}$cm.
分析 根据题意点A2落在A3的位置时,点A旋转了3次,第一次以D点为圆心,4cm为半径,圆心角为60°,第二次以C1点为圆心,4$\sqrt{3}$cm为半径,圆心角为120°,第三次以B2点为圆心,4cm为半径,圆心角为60°,求三次旋转的弧长即可.
解答  解:连接BC1,∵四边形ABCD为菱形,∠BAD=60°,
解:连接BC1,∵四边形ABCD为菱形,∠BAD=60°,
∴∠ABC1=90°,∠AC1B=30°,
∵AB=4cm,
∴BC1=4$\sqrt{3}$cm,
点A落在点A1的经过的路径长为$\frac{60π×4}{180}$=$\frac{4π}{3}$cm,
点A1落在点A2的经过的路径长为$\frac{120π×4\sqrt{3}}{180}$=$\frac{8\sqrt{3}}{3}π$cm,
点A2落在点A3的经过的路径长为
∴点A在旋转过程中经过的路径长为$\frac{8+8\sqrt{3}}{3}$cm.
故答案为$\frac{8+8\sqrt{3}}{3}$.
点评 本题考查了弧长公式的计算,旋转的性质,菱形的性质,熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键.

练习册系列答案
相关题目
3. 如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )
如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )
 如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )
如图,每个小正方形的边长都相等,A、B、C是小正方形的顶点,则∠ABC的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
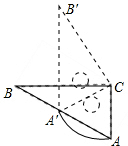 如图,Rt△ABC中,∠B=30°,斜边AB长12为cm,绕直角顶点C顺时针旋转,当点A落在AB边上的A′处,则弧AA′的长为2π cm.(结果保留π)
如图,Rt△ABC中,∠B=30°,斜边AB长12为cm,绕直角顶点C顺时针旋转,当点A落在AB边上的A′处,则弧AA′的长为2π cm.(结果保留π)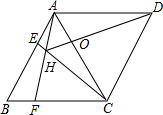 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( ) 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,点A为⊙O上一动点,弦AB过点P,则AB最长为6,AB最短为2$\sqrt{6}$.
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,点A为⊙O上一动点,弦AB过点P,则AB最长为6,AB最短为2$\sqrt{6}$.