题目内容
20.已知二次函数y=-x2+bx+c,函数值y与自变量x之间的部分对应值如表:| x | … | -4 | -1 | 0 | 1 | … |
| y | … | -2 | 1 | -2 | -7 | … |
(2)求二次函数的表达式.
(3)当-4<x<-1时,写出函数值y的取值范围.
分析 (1)根据抛物线的对称性,x=-4、x=0时的函数值相等,然后列式计算即可得解;
(2)待定系数法求解可得;
(3)根据二次函数的性质可得.
解答 解:(1)∵x=-4、x=0时的函数值相等,都是-2,
∴此函数图象的对称轴为直线x=$\frac{-4+0}{2}$=-2;
(2)将(-1,1)、(0,-2)代入y=-x2+bx+c,
得:$\left\{\begin{array}{l}{-1-b+c=1}\\{c=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-4}\\{c=-2}\end{array}\right.$,
∴二次函数的表达式为:y=-x2-4x-2;
(3)∵y=-x2-4x-2=-(x+2)2+2,
∴当x=-2时,y取得最大值2,
由表可知当x=-4时y=-2,当x=-1时y=1,
∴当-4<x<-1时,-2<y≤2.
点评 本题考查了二次函数图象与性质及待定系数法求函数解析式,熟练掌握二次函数的图象与性质是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
15. 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | 直线OM与直线MN是同一条直线 | B. | 射线MO与射线MN是同一条射线 | ||
| C. | 线段OM与线段ON是同一条线段 | D. | 射线NO与射线MO是同一条射线 |
 如图,直线AB、CD相交于点O,∠AOC=70°,OE把∠BOD分成两个角.且∠BOE:∠EOD=2:3,求∠EOD的度数.
如图,直线AB、CD相交于点O,∠AOC=70°,OE把∠BOD分成两个角.且∠BOE:∠EOD=2:3,求∠EOD的度数.
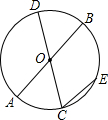 如图,已知AB和CD为⊙O的两条直径,弦CE∥AB,$\widehat{EC}$的度数为40°,求∠BOD的度数.
如图,已知AB和CD为⊙O的两条直径,弦CE∥AB,$\widehat{EC}$的度数为40°,求∠BOD的度数.