题目内容
10．解方程：（1）3（x-2）2=x（x-2）
（2）x2-2x-3=0．
分析 （1）移项后提取公因式法分解因式，再求解可得；
（2）十字相乘法分解因式，再求解可得．
解答 解：（1）∵3（x-2）2-x（x-2）=0，
∴（x-2）（3x-6-x）=0，即（x-2）（2x-6）=0，
∴x-2=0或2x-6=0，
解得：x=2或x=3；
（2）∵（x+1）（x-3）=0，
∴x+1=0或x-3=0，
解得：x=-1或x=3．
点评 本题考查了一元二次方程的解法．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法．
练习册系列答案
相关题目
1．下列各式由左边到右边的变形中，是因式分解的是（ ）
| A． | a2-3a+2=a（a-3） | B． | a2x-a=a（ax-1） | C． | x2+3x+9=（x+3）2 | D． | （x+1）（x-1）=x2-1 |
18．今天教室温度是8℃，室外温度是零下6℃，则室内外温差（ ）
| A． | 2℃ | B． | 12℃ | C． | 14℃ | D． | 16℃ |
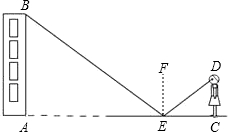小红用下面的方法来测量学校教学大楼AB的高度：如图，在水平地面点E处放一面平面镜，镜子与教学大楼的距离AE=20m．当她与镜子的距离CE=2.5m时，她刚好能从镜子中看到教学大楼的顶端B．已知她的眼睛距地面高度DC=1.5m，请你帮助小红计算大楼的高度．
20．已知二次函数y=-x2+bx+c，函数值y与自变量x之间的部分对应值如表：
（1）写出二次函数图象的对称轴．
（2）求二次函数的表达式．
（3）当-4＜x＜-1时，写出函数值y的取值范围．
| x | … | -4 | -1 | 0 | 1 | … |
| y | … | -2 | 1 | -2 | -7 | … |
（2）求二次函数的表达式．
（3）当-4＜x＜-1时，写出函数值y的取值范围．