题目内容
20.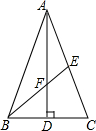 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AD=18,点E在AC上且CE=$\frac{1}{2}$AC,连接BE,与AD相交于点F.若BE=15,则△DBF的周长是24.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AD=18,点E在AC上且CE=$\frac{1}{2}$AC,连接BE,与AD相交于点F.若BE=15,则△DBF的周长是24.
分析 根据等腰三角形三线合一的性质得出BD=CD,又由CE=$\frac{1}{2}$AC,可知F是△ABC的重心,根据重心的性质得出BF=$\frac{2}{3}$BE=10,DF=$\frac{1}{3}$AD=6,在Rt△BDF中利用勾股定理求出BD,进而得出△DBF的周长.
解答 解:∵在△ABC中,AB=AC,AD⊥BC,
∴AD是△ABC的中线,
∵CE=$\frac{1}{2}$AC,即BE是△ABC的中线,
∵BE与AD相交于点F,
∴F是△ABC的重心,
∴BF=$\frac{2}{3}$BE=10,DF=$\frac{1}{3}$AD=6.
在Rt△BDF中,∵∠BDF=90°,
∴BD=$\sqrt{B{F}^{2}-D{F}^{2}}$=8,
∴△DBF的周长=BD+DF+BF=8+6+10=24.
故答案为24.
点评 本题考查了三角形重心的性质:重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查了等腰三角形三线合一的性质,勾股定理,重心的定义,得出F是△ABC的重心是解题的关键.

练习册系列答案
相关题目
15.下列数据不能确定物体位置的是( )
| A. | 北偏东30° | B. | 祥云花园4楼8号 | ||
| C. | 希望路25号 | D. | 东经118°,北纬40° |
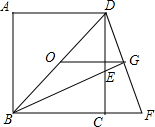 已知:如图,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
已知:如图,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.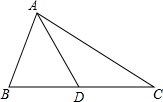 已知如图,△ABC中,AB<AC,D是BC中点,求证:∠CAD<∠BAD.
已知如图,△ABC中,AB<AC,D是BC中点,求证:∠CAD<∠BAD.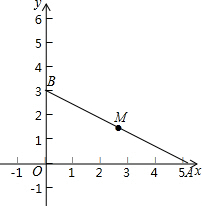 已知一次函数分别交x,y轴于点A(3$\sqrt{3}$,0),B(0,3),点M是AB的中点.
已知一次函数分别交x,y轴于点A(3$\sqrt{3}$,0),B(0,3),点M是AB的中点. 如图,平行四边形ABCD中,BM=4,且AM=5,BD=12,AD=9,则ABCD的面积是$\frac{540}{13}$.
如图,平行四边形ABCD中,BM=4,且AM=5,BD=12,AD=9,则ABCD的面积是$\frac{540}{13}$.