题目内容
4. 如图,已知一艘渔船上的渔民在B处看见灯塔M在北偏东27°方向,这艘渔船以28海里/时的速度向正西方向航行,半小时后到达A处,在A处看见灯塔M在北偏东60°方向,请你运用以上测得的数据求出此时灯塔M与渔船的距离.
如图,已知一艘渔船上的渔民在B处看见灯塔M在北偏东27°方向,这艘渔船以28海里/时的速度向正西方向航行,半小时后到达A处,在A处看见灯塔M在北偏东60°方向,请你运用以上测得的数据求出此时灯塔M与渔船的距离.(结果精确到0.1海里,参考数据:$\sqrt{3}$≈1.732,sin33°≈0.5446,cos33°=0.8387,tan33°=0.6494)
分析 作BC⊥AM于C,根据直角三角形的性质分别求出BC、AC的长,根据正切的概念求出CM,计算即可.
解答 解:作BC⊥AM于C,
AB=28×0.5=14海里,
由题意得,∠CAB=30°,
则BC=$\frac{1}{2}$AB=7,AC=7$\sqrt{3}$,
∠M=60°-27°=33°,
MC=$\frac{BC}{tan∠M}$≈10.78,
AM=AC+CM=7$\sqrt{3}$+10.78≈23.0海里,
答:灯塔M与渔船的距离约为23.0海里.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
15.下列数据不能确定物体位置的是( )
| A. | 北偏东30° | B. | 祥云花园4楼8号 | ||
| C. | 希望路25号 | D. | 东经118°,北纬40° |
13.用代入法解方程组$\left\{\begin{array}{l}{3x=2y+1}&\\{2x=3y}&\end{array}\right.$,以下各式中,代入正确的是( )
| A. | 3x=2×$\frac{2x}{3}$+1 | B. | 3x=2×$\frac{2y}{3}$+1 | C. | 3x=2×$\frac{3x}{2}$+1 | D. | 3x=2×6x+1 |
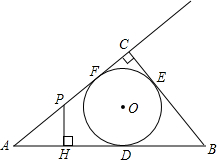 如图,Rt△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.
如图,Rt△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.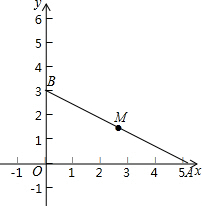 已知一次函数分别交x,y轴于点A(3$\sqrt{3}$,0),B(0,3),点M是AB的中点.
已知一次函数分别交x,y轴于点A(3$\sqrt{3}$,0),B(0,3),点M是AB的中点. 如图,平行四边形ABCD中,BM=4,且AM=5,BD=12,AD=9,则ABCD的面积是$\frac{540}{13}$.
如图,平行四边形ABCD中,BM=4,且AM=5,BD=12,AD=9,则ABCD的面积是$\frac{540}{13}$.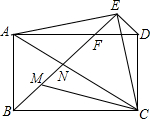 如图,矩形ABCD中,AB=3,AD=4,△ACE为等腰直角三角形,∠AEC=90°,连接BE交AD、AC分别于F、N,CM平分∠ACB交BN于M,则MN:NF=5:9.
如图,矩形ABCD中,AB=3,AD=4,△ACE为等腰直角三角形,∠AEC=90°,连接BE交AD、AC分别于F、N,CM平分∠ACB交BN于M,则MN:NF=5:9.