题目内容
17.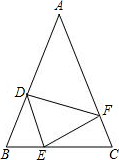 如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.(1)求证:DE=EF;
(2)当∠A=44°时,求∠DEF的度数;
(3)当∠A等于多少度时,△DEF成为等边三角形?试证明你的结论.
分析 (1)根据AB=AC可得∠B=∠C,即可求证△BDE≌△CEF,即可解题;
(2)根据全等三角形的性质,得出∠BED=∠CFE,再根据三角形内角和定理以及平角的定义,即可求得∠DEF的度数;
(3)根据△DEF为等边三角形,以及△BDE≌△CEF,可得∠C的度数,最后根据等腰三角形ABC,求得其顶角的度数.
解答  解:(1)∵AB=AC,
解:(1)∵AB=AC,
∴∠B=∠C,
∵在△BDE和△CEF中,
$\left\{\begin{array}{l}{BD=CE}\\{∠B=∠C}\\{BE=CF}\end{array}\right.$,
∴△BDE≌△CEF(SAS),
∴DE=EF;
(2)当∠A=44°时,∠B=∠C=$\frac{1}{2}$(180°-44°)=68°,
∵△BDE≌△CEF,
∴∠BED=∠CFE,
∵△CEF中,∠CEF+∠CFE=180°-68°=112°,
∴∠BED+∠CEF=112°,
∴∠DEF=180°-112°=68°;
(3)当∠A等于60度时,△DEF成为等边三角形.
证明:若△DEF为等边三角形,则∠DEF=60°,
∴∠BED+∠CEF=120°,
又∵△BDE≌△CEF,
∴∠BED=∠CFE,
∴△CEF中,∠CEF+∠CFE=120°,
∴∠C=180°-120°=60°=∠B,
∴△ABC中,∠A=180°-60°×2=60°.
点评 本题属于三角形综合题,主要考查了等腰三角形的性质,等边三角形的判定与性质以及全等三角形的判定与性质的综合应用,解决问题的关键是运用全等三角形的对应边相等,对应角相等进行计算推导,解题时注意三角形的内角和等于180°.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
7.若点M(m,n)(mn≠0)在二次函数y=ax2(a≠0)图象上,则下列坐标表示的点也在该抛物线图象上的是( )
| A. | (-m,n) | B. | (n,m) | C. | (m2,n2) | D. | (m,-n) |
8. 如图,AB∥CD,∠E=37°,∠C=20°,则∠EAB=( )
如图,AB∥CD,∠E=37°,∠C=20°,则∠EAB=( )
 如图,AB∥CD,∠E=37°,∠C=20°,则∠EAB=( )
如图,AB∥CD,∠E=37°,∠C=20°,则∠EAB=( )| A. | 37° | B. | 20° | C. | 17° | D. | 57° |
5.对于a>b>c>0,m>n>0(m、n是正整数),成立的关系式是( )
| A. | ambn>bncm>cnam | B. | ambn>cnam>bncm | C. | amcn>ambn>bncm | D. | bnam>cnam>ambn |
2.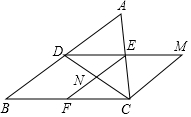 如图,在三边互不相等的△ABC中,D、E、F分别是AB、AC、BC边的中点,连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
如图,在三边互不相等的△ABC中,D、E、F分别是AB、AC、BC边的中点,连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
 如图,在三边互不相等的△ABC中,D、E、F分别是AB、AC、BC边的中点,连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
如图,在三边互不相等的△ABC中,D、E、F分别是AB、AC、BC边的中点,连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
6.下列运算正确的是( )
| A. | x3•x4=x12 | B. | (-6x4)÷(-2x2)=3x3 | C. | (-2a2)2=4a4 | D. | (x-3)2=x2-9 |
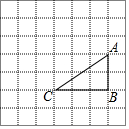 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.则A1的坐标为(-1,4).
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.则A1的坐标为(-1,4).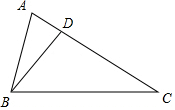 如图,∠ABD=∠C,AD=4,CD=6,求△ABC与△ADB的周长比与面积比.
如图,∠ABD=∠C,AD=4,CD=6,求△ABC与△ADB的周长比与面积比.