题目内容
7．若点M（m，n）（mn≠0）在二次函数y=ax2（a≠0）图象上，则下列坐标表示的点也在该抛物线图象上的是（ ）| A． | （-m，n） | B． | （n，m） | C． | （m2，n2） | D． | （m，-n） |
分析 利用二次函数图象的对称性即可解决．
解答 解：∵二次函数y=ax2（a≠0）的对称轴是y轴，
∴点M（m，n）（mn≠0）关于y轴的对称点（-m，n）也在该抛物线图象上，
故选：A．
点评 本题主要考查二次函数图象与系数的关系，掌握①二次项系数a决定抛物线的开口方向和大小，②一次项系数b和二次项系数a共同决定对称轴的位置，③常数项c决定抛物线与y轴交点，④抛物线与x轴交点个数是解题的关键．
练习册系列答案
相关题目
17．已知开口向下的抛物线y=ax2-3x+a2-2a-3经过坐标原点，那么a等于（ ）
| A． | -1 | B． | 3 | C． | -3 | D． | 3或-1 |
18．已知3x=5y（y≠0），则下列比例式成立的是（ ）
| A． | $\frac{x}{3}$=$\frac{5}{y}$ | B． | $\frac{x}{5}$=$\frac{y}{3}$ | C． | $\frac{x}{y}$=$\frac{3}{5}$ | D． | $\frac{x}{3}$=$\frac{y}{5}$ |
15．抛物线y=（x+1）2+2的顶点是（ ）
| A． | （1，2） | B． | （-1，2） | C． | （-1，-2） | D． | （1，-2） |
2．
如图，PA、PB、AB都与⊙O相切，∠P=60°，则∠AOB等于（ ）
如图，PA、PB、AB都与⊙O相切，∠P=60°，则∠AOB等于（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 70° |
19．下列各组单项式中，不是同类项的一组是（ ）
| A． | x2y和2xy2 | B． | -32和3 | C． | 3xy和-$\frac{xy}{2}$ | D． | 5x2y和-2yx2 |
16．
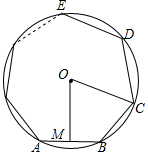如图，点M是⊙O内接正n边形ABCDE…边AB的中点，连接OM、OC，则∠MOC的度数为（ ）
如图，点M是⊙O内接正n边形ABCDE…边AB的中点，连接OM、OC，则∠MOC的度数为（ ）| A． | 180°-$\frac{360°}{n}$ | B． | $\frac{360°}{n}$ | C． | $\frac{540°}{n}$ | D． | $\frac{720°}{n}$ |
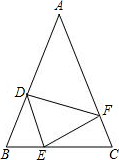如图，在△ABC中，AB=AC，点D，E，F分别在AB，BC，AC边上，且BE=CF，BD=CE．