题目内容
6.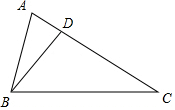 如图,∠ABD=∠C,AD=4,CD=6,求△ABC与△ADB的周长比与面积比.
如图,∠ABD=∠C,AD=4,CD=6,求△ABC与△ADB的周长比与面积比.
分析 根据相似三角形的判定和性质即可得到结论.
解答 解:∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,
∴$\frac{AB}{AC}=\frac{AD}{AB}$,
∴AB2=AD•AC=40,
∴AB=2$\sqrt{10}$,
∴△ABC与△ADB的周长比=$\frac{AB}{AD}$=$\frac{\sqrt{10}}{2}$,△ABC与△ADB的面积比=($\frac{AB}{AD}$)2=$\frac{5}{2}$.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
1.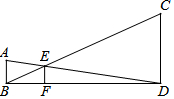 如图,AB、CD、EF都与BD垂直,且AB=1,CD=3,那么EF的长是( )
如图,AB、CD、EF都与BD垂直,且AB=1,CD=3,那么EF的长是( )
 如图,AB、CD、EF都与BD垂直,且AB=1,CD=3,那么EF的长是( )
如图,AB、CD、EF都与BD垂直,且AB=1,CD=3,那么EF的长是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
16.化简$\frac{2}{{x}^{2}-1}$÷$\frac{1}{x-1}$的结果是( )
| A. | $\frac{2}{x-1}$ | B. | $\frac{2}{x}$ | C. | $\frac{2}{x+1}$ | D. | 2(x+1) |
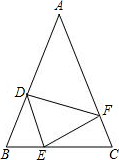 如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE. 如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F.如果AB=6,BC=10,那么$\frac{DE}{DF}$的值是$\frac{3}{8}$.
如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F.如果AB=6,BC=10,那么$\frac{DE}{DF}$的值是$\frac{3}{8}$.