题目内容
2.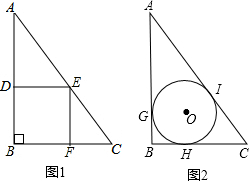 如图,有一块三角形余料ABC,∠B=90°,BC=3m,AB=4m,现有两种余料的再利用方案,分别制作正方形和圆形桌面.
如图,有一块三角形余料ABC,∠B=90°,BC=3m,AB=4m,现有两种余料的再利用方案,分别制作正方形和圆形桌面.方案一,如图1,作正方形DEFG使它的四个顶点都在△ABC边上;
方案二,如图2,作△ABC的内切圆O,它与三边分别相切与点G、H、I.
请通过计算,比较哪种方案的利用率高.
分析 设DE=x,再由相似三角形的性质得出x的长,进而可得出正方形DBFE的面积;先根据勾股定理求出AC的长,再连接OA,OB,OC,OG,OI,OH由三角形的面积公式得出⊙O的半径,求出圆的面积,进而可得出结论.
解答 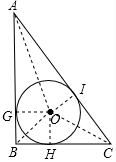 解:设DE=x,则AD=4-x,
解:设DE=x,则AD=4-x,
∵DE⊥AB,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$,即$\frac{4-x}{4}$=$\frac{x}{3}$,解得x=$\frac{12}{7}$,
∴S正方形=($\frac{12}{7}$)2=$\frac{144}{49}$;
∵△ABC中,∠B=90°,BC=3m,AB=4m,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5m.
∵点O是△ABC的内心,
∴OI=OG=OH=r,
∴$\frac{1}{2}$(AB+BC+AC)•r=$\frac{1}{2}$AB•BC,即(4+3+5)r=4×3,解得r=1,
∴S⊙O=π.
∵$\frac{144}{49}$<π,
∴方案二利用率高.
点评 本题考查的是三角形的内切圆与内心,熟知三角形的内心就是三角形三个内角角平分线的交点是解答此题的关键.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
12.已知P1(-3,y1)、P2(-2,y2)是二次函数y=-2(x+1)2+1图象上的两个点,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1≤y2 | C. | y1>y2 | D. | 无法确定 |
7. 实数a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
实数a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
 实数a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
实数a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )| A. | 2a-b | B. | b | C. | -b | D. | -2a+b |
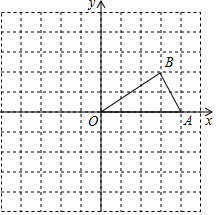 如图,已知点A,B的坐标分别为(4,0),(3,2).
如图,已知点A,B的坐标分别为(4,0),(3,2). 如图,在菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上,得到经过点D的折痕DE,则∠CDE的度数为45°.
如图,在菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上,得到经过点D的折痕DE,则∠CDE的度数为45°.