题目内容
11. 如图,在菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上,得到经过点D的折痕DE,则∠CDE的度数为45°.
如图,在菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上,得到经过点D的折痕DE,则∠CDE的度数为45°.
分析 连接BD,由菱形的性质及∠A=60°,得到三角形ABD为等边三角形,P为AB的中点,利用三线合一得到DP为角平分线,得到∠ADP=30°,∠ADC=120°,∠C=60°,进而求出∠PDC=90°,由折叠的性质得到∠CDE=∠PDE=45°.
解答 解:连接BD,
∵四边形ABCD为菱形,∠A=60°,
∴△ABD为等边三角形,∠ADC=120°,∠C=60°,
∵P为AB的中点,
∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,
∴∠PDC=90°,
∴由折叠的性质得到∠CDE=∠PDE=45°
故答案为:45°
点评 此题考查了翻折变换(折叠问题),菱形的性质,等边三角形的性质,以及内角和定理,熟练掌握折叠的性质是解本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
16.已知长方形的周长为20cm,设它的长为x cm,则它的宽为( )
| A. | (20-x)cm | B. | $\frac{20-x}{2}cm$ | C. | (20-2x)cm | D. | (10-x)cm |
20.下列运算中,正确的是( )
| A. | 3a+5b=15ab | B. | (a2)3=a9 | C. | a6-a2=a4 | D. | 2a×3a=6a2 |
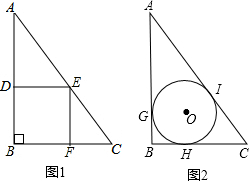 如图,有一块三角形余料ABC,∠B=90°,BC=3m,AB=4m,现有两种余料的再利用方案,分别制作正方形和圆形桌面.
如图,有一块三角形余料ABC,∠B=90°,BC=3m,AB=4m,现有两种余料的再利用方案,分别制作正方形和圆形桌面.