题目内容
5.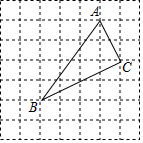 如图,在7×7网格中,每个小正方形的边长都为1.
如图,在7×7网格中,每个小正方形的边长都为1.(1)建立适当的平面直角坐标系,使点A(3,4)、C(4,2),则点B的坐标为(0,0);
(2)求图中格点△ABC的面积;
(3)判断格点△ABC的形状,并说明理由.
(4)在x轴上有一点P,使得PA+PC最小,则PA+PC的最小值是$\sqrt{17}$.
分析 (1)首先根据A和C的坐标确定坐标轴的位置,然后确定B的坐标;
(2)利用矩形的面积减去三个直角三角形的面积求解;
(3)利用勾股定理的逆定理即可作出判断;
(4)作点C关于x轴的对称点C′连接AC′交x轴与点P,连接PC,依据轴对称图形的性质可得到PC=PC′,然后依据两点之间线段最短可知当点A,P,C′在一条直线上时,AP+PC有最小值.
解答 解:(1)B的坐标是(0,0).
故答案是(0,0);
(2)S△ABC=4×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×3×4-$\frac{1}{2}$×1×2=5,
(3)∵AC2=22+12=5,BC2=22+42=20,AB2=42+32=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
(4)如图1所示:作点C关于x轴的对称点C′连接AC′交x轴与点P,连接PC.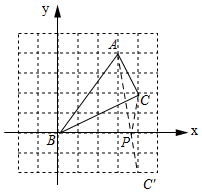
∵点C与点C′关于x轴对称,
∴PC=PC′.
∴AP+PC=AP+PC.
∴当A,P,C′在一条直线上时,AP+PC有最小值,最小值为AC′的长.
∵AC′=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$.
∴AP+PC的最小值为$\sqrt{17}$.
故答案为:$\sqrt{17}$.
点评 本题主要考查的是轴对称路径最短问题、勾股定理的应用,勾股定理的逆定理的应用,明确点A,P,C′在一条直线上时,AP+PC有最小值是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列说法:
①两点之间的所有连线中,线段最短;
②在数轴上与表示-1的点距离是3的点表示的数是2;
③连接两点的线段叫做两点间的距离;
④若AC=BC,则点C是线段AB的中点;
⑤一条射线把一个角分成两个相等的角,这条射线是这个角的平分线.
其中错误的有( )
①两点之间的所有连线中,线段最短;
②在数轴上与表示-1的点距离是3的点表示的数是2;
③连接两点的线段叫做两点间的距离;
④若AC=BC,则点C是线段AB的中点;
⑤一条射线把一个角分成两个相等的角,这条射线是这个角的平分线.
其中错误的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
14.已知3是关于x的方程x2-5x+c=0的一个根,则这个方程的另一个根是( )
| A. | -2 | B. | 2 | C. | 5 | D. | 6 |
 如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,连接AD.
如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,连接AD.
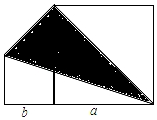 如图中大、小正方形的边长分别为a和2(a>2);
如图中大、小正方形的边长分别为a和2(a>2);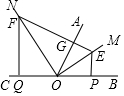 如图,O是直线BC上的 点,OM平分∠AOB,ON平分∠AOC,点E在OM上,过点E作EG⊥OA于点G,EP⊥OB于点P,延长EG,交ON于点F,过点F作FQ⊥OC于点Q,若EF=10,则FQ+EP的长度为( )
如图,O是直线BC上的 点,OM平分∠AOB,ON平分∠AOC,点E在OM上,过点E作EG⊥OA于点G,EP⊥OB于点P,延长EG,交ON于点F,过点F作FQ⊥OC于点Q,若EF=10,则FQ+EP的长度为( )