题目内容
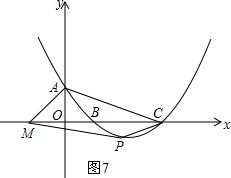
1.王先生开轿车从A地出发,前往B地,路过服务区休息一段时间后,继续以原速度行驶,到达B地后,又休息了一段时间,然后开轿车按原路返回A地,速度是原来的1.2倍.王先生距离A地的路程y(km)与行驶的时间x(h)之间的函数图象如图所示.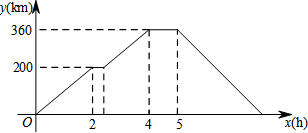
(1)王先生开轿车从A地行驶到B地的途中,休息了0.4h;
(2)求王先生开轿车从B地返回A地时y与x之间的函数关系式(不要求写出自变量x的取值范围);
(3)王先生从B地返回A地的途中,再次经过从A地到B地时休息的服务区,求此时的x的值.
分析 (1)根据原速度行驶,得出从A地行驶到B地的途中休息的时间;
(2)根据计算得出两个点的坐标,再代入y=kx+b中,得出函数解析式即可;
(3)把y=200代入解析式解答即可.
解答 解:(1)因为按原速度行驶,设休息后到达B地再走xh,
所以可得$\frac{200}{2}=\frac{360-200}{x}$,
解得:x=1.6,
经检验x=1.6是方程的解,
所以休息时间为4-2-1.6=0.4;
故答案为:0.4;
(2)如图,王先生从B地返回A地的速度是200÷2×1.2=120,所用时间为360÷120=3.
∴图象经过点(8,0).
设y与x之间的函数关系式为y=kx+b(k≠0).
由题意,得$\left\{\begin{array}{l}5k+b=360\\ 8k+b=0.\end{array}\right.$
解得$\left\{\begin{array}{l}k=-120\\ b=960.\end{array}\right.$
∴y与x之间的函数关系式为y=-120x+960.
(3)当y=200时,200=-120x+960.
解得$x=\frac{19}{3}$.
答:当$x=\frac{19}{3}$时,王先生再次经过从A地到B地时休息的服务区.
点评 此题考查一次函数的应用,关键是根据实际问题并结合函数的图象得到进一步解题的有关信息,并从实际问题中整理出一次函数模型.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
12.下列说法正确的是( )
| A. | 一组数据8,8,7,10,6,8,9的众数和中位数都是8 | |
| B. | 为了解全国中学生的心理健康情况,应该采用普查的方式 | |
| C. | 一个游戏的中奖概率是0.1,则做10次这样的游戏一定会中奖 | |
| D. | 若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定 |
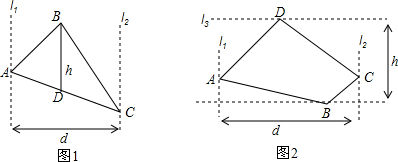
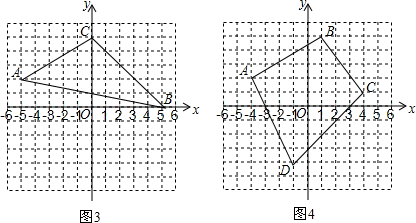
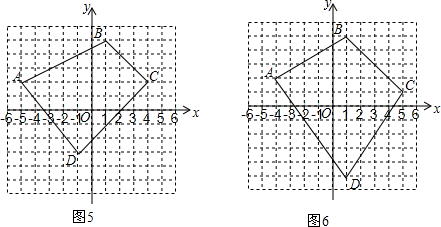
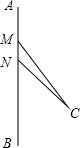 “村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)
“村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)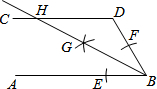 如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为32度.
如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为32度.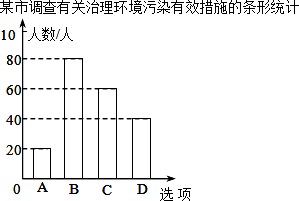 某市对市民进行了有关“治理环境污染”的问卷调查,调查问卷内容是“你认为下列哪种治理环境污染的措施最有效?”有以下四个选项(每份调查问卷必答且只选一个选项):
某市对市民进行了有关“治理环境污染”的问卷调查,调查问卷内容是“你认为下列哪种治理环境污染的措施最有效?”有以下四个选项(每份调查问卷必答且只选一个选项):
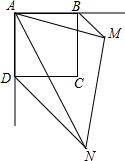 已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.
已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.