题目内容
 如图在Rt△ABC中,∠ACB=90°,AC=3,BC=4,则既平分△ABC周长又平分△ABC面积的直线有几条?
如图在Rt△ABC中,∠ACB=90°,AC=3,BC=4,则既平分△ABC周长又平分△ABC面积的直线有几条?考点:面积及等积变换,勾股定理,相似三角形的判定与性质
专题:分类讨论
分析:可运用勾股定理求出AB长,从而求出△ABC周长和面积;设既平分△ABC周长又平分△ABC面积的直线为m,可分三种情况(①直线m与边BC和边AB相交,②直线m与边AC和边AB相交,③直线m与边AC和边BC相交)进行讨论,然后只需根据条件建立方程,求出符合要求的未知数的值,就可解决问题.
解答:解:∵∠ACB=90°,AC=3,BC=4,
∴AB=
=5,
∴△ABC的周长为12,△ABC的面积=
×3×4=6.
设既平分△ABC周长又平分△ABC面积的直线为m,
①若直线m与边BC交于点P,与边AB交于点Q,过点P作PG⊥AB于G,设PB=x,如图1,
则∠PGB=∠C=90°,BQ=
-x=6-x,(0<x≤4),S△PQB=
S△ABC=3,
∵∠B=∠B,∠PGB=∠C,
∴△PGB∽△ACB,
∴
=
,
∴
=
,
∴PG=
x,
∴S△PQB=
BQ•PG=
(6-x)•
x=3,
整理得:x2-6x+10=0.
∵△=(-6)2-4×1×10=-4<0,
∴方程无解;
② 若直线m与边AC交于点D,与边AB交于点E,过点D作DH⊥AB于H,设AD=y,如图2,
若直线m与边AC交于点D,与边AB交于点E,过点D作DH⊥AB于H,设AD=y,如图2,
则∠AHD=∠C=90°,AE=
-x=6-y,(0<y≤3),S△ADE=
S△ABC=3,
同理可得:DH=
y,
∴S△ADE=
AE•DH=
(6-y)•
y=3,
整理得:2y2-12y+15=0.
∵△=(-12)2-4×2×15=24>0,
∴y=
=3±
.
∵0<y≤3,
∴y=3-
;
③ 若直线m与边AC交于点M,与边BC交于点N,设CM=m,如图3,
若直线m与边AC交于点M,与边BC交于点N,设CM=m,如图3,
则CN=
-m=6-m,(0<m≤3),S△CMN=
S△ABC=3,
∴
m(6-m)=3,
整理得:m2-6m+6=0.
∵△=(-6)2-4×1×6=12>0,
∴m=
=3±
.
∵0<m≤3,
∴m=3-
.
综上所述:既平分△ABC周长又平分△ABC面积的直线有2条.
∴AB=
| AC2+BC2 |
∴△ABC的周长为12,△ABC的面积=
| 1 |
| 2 |
设既平分△ABC周长又平分△ABC面积的直线为m,
①若直线m与边BC交于点P,与边AB交于点Q,过点P作PG⊥AB于G,设PB=x,如图1,
则∠PGB=∠C=90°,BQ=
| 12 |
| 2 |
| 1 |
| 2 |
∵∠B=∠B,∠PGB=∠C,

∴△PGB∽△ACB,
∴
| PG |
| AC |
| PB |
| AB |
∴
| PG |
| 3 |
| x |
| 5 |
∴PG=
| 3 |
| 5 |
∴S△PQB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
整理得:x2-6x+10=0.
∵△=(-6)2-4×1×10=-4<0,
∴方程无解;
②
 若直线m与边AC交于点D,与边AB交于点E,过点D作DH⊥AB于H,设AD=y,如图2,
若直线m与边AC交于点D,与边AB交于点E,过点D作DH⊥AB于H,设AD=y,如图2,则∠AHD=∠C=90°,AE=
| 12 |
| 2 |
| 1 |
| 2 |
同理可得:DH=
| 4 |
| 5 |
∴S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
整理得:2y2-12y+15=0.
∵△=(-12)2-4×2×15=24>0,
∴y=
12±
| ||
| 2×2 |
| ||
| 2 |
∵0<y≤3,
∴y=3-
| ||
| 2 |
③
 若直线m与边AC交于点M,与边BC交于点N,设CM=m,如图3,
若直线m与边AC交于点M,与边BC交于点N,设CM=m,如图3,则CN=
| 12 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
整理得:m2-6m+6=0.
∵△=(-6)2-4×1×6=12>0,
∴m=
6±
| ||
| 2×1 |
| 3 |
∵0<m≤3,
∴m=3-
| 3 |
综上所述:既平分△ABC周长又平分△ABC面积的直线有2条.
点评:本题主要考查了勾股定理、相似三角形的判定与性质、运用公式法解一元二次方程、根的判别式、三角形的面积公式等知识,运用分类讨论的思想是解决本题的关键,需要注意的是:解方程后,应根据未知数的取值范围进行取舍.

练习册系列答案
相关题目
方程x2-6x-1=0,经配方后得方程为( )
A、(x-3)2=
| ||
B、(x+3)2=
| ||
| C、(x+3)2=10 | ||
| D、(x-3)2=10 |
 一次函数y=kx+b的图象如图所示,当y<5时,x的取值范围是
一次函数y=kx+b的图象如图所示,当y<5时,x的取值范围是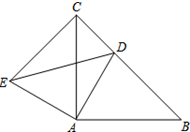 已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.
已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点. 如图1,△ABC中,∠ACB=90°,CE⊥AB于E,D在线段AB上,AD=AC,AF平分∠CAE交CE于F.
如图1,△ABC中,∠ACB=90°,CE⊥AB于E,D在线段AB上,AD=AC,AF平分∠CAE交CE于F.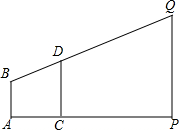 如图所示,旗杆顶部Q,标杆顶部D,观测者的眼睛B在同一直线上,测得观测者的脚到旗杆底部的距离AP=75m,观测者的脚到标杆底部的距离AC=2.5m,若AB=1.5m,标杆CD的高为2m,那么旗杆有多高.
如图所示,旗杆顶部Q,标杆顶部D,观测者的眼睛B在同一直线上,测得观测者的脚到旗杆底部的距离AP=75m,观测者的脚到标杆底部的距离AC=2.5m,若AB=1.5m,标杆CD的高为2m,那么旗杆有多高.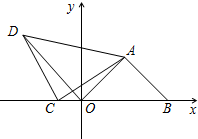 如图,在平面直角坐标系中,△AOB为等腰直角三角形,AB=OA,B(8,0),C为x轴负半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连OD.
如图,在平面直角坐标系中,△AOB为等腰直角三角形,AB=OA,B(8,0),C为x轴负半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连OD.