题目内容
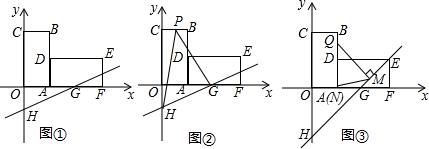
20.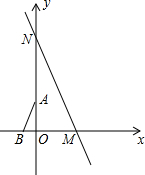 如图,在直角坐标系中,直线y=-$\sqrt{3}x+5\sqrt{3}$分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=60°,AB=2,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)或($\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
如图,在直角坐标系中,直线y=-$\sqrt{3}x+5\sqrt{3}$分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=60°,AB=2,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)或($\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
分析 先确定∠NMO=60°,再计算出OA=$\sqrt{3}$,然后利用AB与直线MN平行画出图形,直线AB交x轴于点C,作AH⊥x轴于H,则∠OCB=60°,再利用含30度的直角三角形三边的关系求AH、OH,从而确定A点坐标.
解答 解:当x=0时,y=-$\sqrt{3}x+5\sqrt{3}$=5$\sqrt{3}$,则N(0,5$\sqrt{3}$),
当y=0时,-$\sqrt{3}x+5\sqrt{3}$=0,解得x=5,则M(5,0),
在Rt△OMN中,∵tan∠NMO=$\frac{5\sqrt{3}}{5}$=$\sqrt{3}$,
∴∠NMO=60°,
在Rt△ABO中,∵∠B=60°,AB=2,
∴∠OAB=30°,
∴OB=1,OA=$\sqrt{3}$,
∵AB与直线MN平行,
∴直线AB与x轴的夹角为60°,
如图1,直线AB交x轴于点C,作AH⊥x轴于H,则∠OCB=60°,
∵∠OCB=∠COA+∠A,
∴∠COA=60°-30°=30°,
在Rt△OAH中,AH=$\frac{1}{2}$OA=$\frac{\sqrt{3}}{2}$,OH=$\sqrt{3}$AH=$\frac{3}{2}$,
∴A点坐标为($\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$);
如图2,直线AB交x轴于点C,作AH⊥x轴于H,则∠OCB=60°,
∵∠OCB=∠COA+∠A,
∴∠COA=60°-30°=30°,
在Rt△OAH中,AH=$\frac{1}{2}$OA=$\frac{\sqrt{3}}{2}$,OH=$\sqrt{3}$AH=$\frac{3}{2}$,
∴A点坐标为(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$);
综上所述,A点坐标为(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)或($\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
故答案为(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)或($\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.解决本题的关键是正确画出旋转后的图形.

 阅读快车系列答案
阅读快车系列答案| A. | 1 | B. | -1 | C. | 0 | D. | (-1)n-1 |
 如图,已知直线a,b,c相交于点O,且a⊥c,垂足为O,若∠1=50°,则∠2的度数为140°.
如图,已知直线a,b,c相交于点O,且a⊥c,垂足为O,若∠1=50°,则∠2的度数为140°.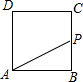 如图,已知正方形ABCD的边长为4,现有一动点P从点B出发,沿着B→C→D→A的路径以每秒1个单位长度的速度运动,则S△PAB与运动时间t(秒)之间的函数关系图象是( )
如图,已知正方形ABCD的边长为4,现有一动点P从点B出发,沿着B→C→D→A的路径以每秒1个单位长度的速度运动,则S△PAB与运动时间t(秒)之间的函数关系图象是( )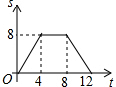
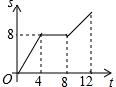
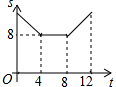
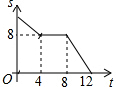
 如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是$\sqrt{3}$.
如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是$\sqrt{3}$.