题目内容
7. 已知:线段c,直线l及l外一点A.
已知:线段c,直线l及l外一点A.求作:Rt△ABC,使直角边AC(AC⊥l,垂足为点C),斜边AB=c.(用尺规作图,写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑).
分析 利用过直线外一点作已知直线的垂线的方法过A作l的垂线,再以A为圆心,c长为半径画弧,交l于B,即可得到Rt△ABC;
解答 解:如图所示:
一、作出垂线段AC,
二、作出线段AB,
三、Rt△ABC就是所求作的三角形.
点评 此题主要考查了复杂作图,关键是掌握过直线外一点作已知直线的垂线的方法,掌握三角形内角和180°.

练习册系列答案
相关题目
9.如果“盈利5%”记作+5%,那么-3%表示( )
| A. | 亏损3% | B. | 亏损8% | C. | 盈利2% | D. | 少赚3% |
18.抛物线y=x2+2x+2-m与x轴有两个交点,则下列m的值符合题意的是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
16.2016年3月,成都市某区一周天气质量报告中某项污染指标的数据是:60,60,100,90,90,70,90,则下列关于这组数据表述正确的是( )
| A. | 众数是60 | B. | 中位数是100 | C. | 平均数是78 | D. | 极差是40 |
17. 某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:
某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:
根据图表信息,回答下列问题:
(1)该班共有学生40人;表中a=20;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.
 某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:
某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:| 类别 | 成绩 | 频数 |
| 甲 | 60≤m<70 | 5 |
| 乙 | 70≤m<80 | a |
| 丙 | 80≤m<90 | 10 |
| 丁 | 90≤m≤100 | 5 |
(1)该班共有学生40人;表中a=20;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.
 在一次数学课上,老师出示了一道题目:
在一次数学课上,老师出示了一道题目: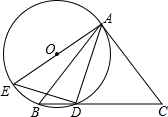 如图,△ABC中,AB=AC,点D为BC边上一点,且DA=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连接DE.
如图,△ABC中,AB=AC,点D为BC边上一点,且DA=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连接DE. 二次函数和y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
二次函数和y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论: