题目内容
10.先化简,再求值,($\frac{{x}^{2}}{x-1}$-x+1)÷$\frac{4{x}^{2}-4x+1}{1-x}$,其中x=$\sqrt{5}$+$\frac{1}{2}$.分析 先算括号里面的,再算除法,最后把x的值代入进行计算即可.
解答 解:原式=$\frac{{x}^{2}-(x-1)^{2}}{x-1}$÷$\frac{(2x-1)^{2}}{1-x}$
=$\frac{{x}^{2}-{x}^{2}+2x-1}{x-1}$•$\frac{1-x}{(2x-1)^{2}}$
=$\frac{2x-1}{x-1}$•$\frac{1-x}{{(2x-1)}^{2}}$
=$\frac{1}{1-2x}$,
当x=$\sqrt{5}$+$\frac{1}{2}$时,原式=$\frac{1}{1-2(\sqrt{5}+\frac{1}{2})}$=$\frac{1}{1-2\sqrt{5}-1}$=-$\frac{\sqrt{5}}{10}$.
点评 本题考查的是分式的化简求值,在解答此类题目时要注意把原式化为最简形式,再代入求值.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
12.钓鱼岛是中国的固有领土,位于中国东海,面积为4400000m2,数据4400000用科学记数法表示为( )
| A. | 4.4×106 | B. | 44×105 | C. | 4×106 | D. | 0.44×107 |
1.sin30°=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.抛物线y=x2+2x+2-m与x轴有两个交点,则下列m的值符合题意的是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
5.盐阜商场试销一种品牌服装,成本为每件300元,规定试销期间销售单价不低于成本单价,且获利不得高于20%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如表:
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
| 销售单价x(元) | … | 330 | 335 | 340 | 345 | … |
| 销售量y(件) | … | 240 | 230 | 220 | 210 | … |
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
 在一次数学课上,老师出示了一道题目:
在一次数学课上,老师出示了一道题目: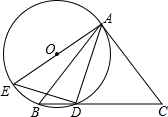 如图,△ABC中,AB=AC,点D为BC边上一点,且DA=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连接DE.
如图,△ABC中,AB=AC,点D为BC边上一点,且DA=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连接DE. 二次函数和y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
二次函数和y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论: