题目内容
15.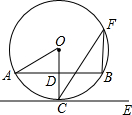 如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )
如图,AB是⊙O的弦,半径OC经过AB的中点D,CE∥AB,点F在⊙O上,连接CF,BF,下列结论中,不正确的是( )| A. | ∠F=$\frac{1}{2}∠AOC$ | B. | AB⊥BF | C. | CE是⊙O的切线 | D. | $\widehat{AC}=\widehat{BC}$ |
分析 分别利用垂径定理以及圆周角定理和切线的判定方法分别分析得出即可.
解答 解:A、∵半径OC经过AB的中点D,
∴$\widehat{AC}$=$\widehat{CB}$,
∴∠F=$\frac{1}{2}∠AOC$,故此结论正确,此选项错误;
B、由于F点不确定,无法得出AB⊥BF,故此选项正确;
C、∵半径OC经过AB的中点D,
∴CO⊥AB,
∵CE∥AB,
∴∠OCE=90°,
∴CE是⊙O的切线,故此结论正确,不合题意;
D、由选项A得,$\widehat{AC}$=$\widehat{CB}$,故此结论正确,此选项错误;
故选:B.
点评 此题主要考查了垂径定理以及圆周角定理和切线的判定方法等知识,正确把握相关性质是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20. 为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.
为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.
(1)填空:x=60,y=80;
(2)在扇形统计图中,C部分所对应的扇形的圆心角是144度;
(3)根据抽样调查结果,请估计该校学生一年阅读课外书20本以上的学生人数.
 为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.
为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.| 各种情况人数统计频数分布表 | ||||
| 课外阅读情况 | A | B | C | D |
| 频数 | 20 | x | y | 40 |
(2)在扇形统计图中,C部分所对应的扇形的圆心角是144度;
(3)根据抽样调查结果,请估计该校学生一年阅读课外书20本以上的学生人数.
7.下列四个实数中,是无理数的是( )
| A. | 0 | B. | -3 | C. | $\frac{1}{7}$ | D. | $\sqrt{8}$ |
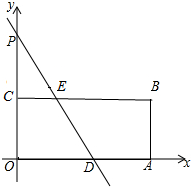 在平面直角坐标系中,矩形OABC的两个顶点坐标分别为A(12,0),B(12,6),已知点P(0,12).
在平面直角坐标系中,矩形OABC的两个顶点坐标分别为A(12,0),B(12,6),已知点P(0,12). 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上的一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上的一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.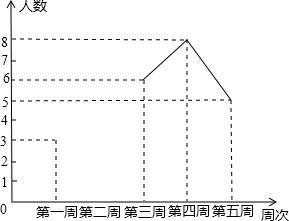 为配合我校开展的“书香校园”活动,校团委对我校某班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:
为配合我校开展的“书香校园”活动,校团委对我校某班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图: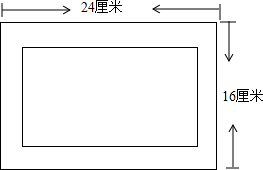 如图,相框的长为24厘米,宽为16厘米,外木缘制边框的宽相等,要使框内部分的面积是整个相框面积$\frac{1}{3}$,则边框的宽应为多少厘米?
如图,相框的长为24厘米,宽为16厘米,外木缘制边框的宽相等,要使框内部分的面积是整个相框面积$\frac{1}{3}$,则边框的宽应为多少厘米?