题目内容
 如图,已知AD、BE是△ABC的高,AD、BE相交于点F,并且AD=BD,你能找到图中的全等三角形吗?若能找到请说明理由.
如图,已知AD、BE是△ABC的高,AD、BE相交于点F,并且AD=BD,你能找到图中的全等三角形吗?若能找到请说明理由.考点:全等三角形的判定
专题:
分析:根据等角的余角相等得到∠CBE=∠CAD,然后根据“ASA”得到△ADC≌△BDF.
解答:解:△ADC≌△BDF,
理由如下:
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BEC=90°,
∴∠CBE=∠CAD,
在△ADC和△BDF中,
,
∴△ADC≌△BDF(ASA).
理由如下:
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BEC=90°,
∴∠CBE=∠CAD,
在△ADC和△BDF中,
|
∴△ADC≌△BDF(ASA).
点评:本题考查了全等三角形的判定,利用有两组角对应相等,并且有一条边对应相等的两个三角形全等是解题关键.

练习册系列答案
相关题目
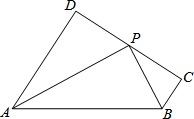 如图,AD∥BC,∠DAB的平分线与∠CBA的平分线交于点P,过点P的直线垂直于AD,垂足为D,交BC于点C.试问:点P是线段CD的中点吗?为什么?
如图,AD∥BC,∠DAB的平分线与∠CBA的平分线交于点P,过点P的直线垂直于AD,垂足为D,交BC于点C.试问:点P是线段CD的中点吗?为什么?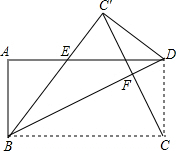 如图,四边形ABCD中,AB=CD,BC=AD,∠A=∠ABC=∠BCD=∠CDA=90°.把它沿着BD折叠,使点C落在C′处,BC′交AD于点E.
如图,四边形ABCD中,AB=CD,BC=AD,∠A=∠ABC=∠BCD=∠CDA=90°.把它沿着BD折叠,使点C落在C′处,BC′交AD于点E. 如图,已知∠AOC:∠BOC=1:3,∠AOD:∠BOD=5:7,若∠COD=15°,求∠AOB的度数.
如图,已知∠AOC:∠BOC=1:3,∠AOD:∠BOD=5:7,若∠COD=15°,求∠AOB的度数. 在?ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.
在?ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.