题目内容
1．
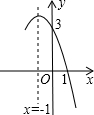已知抛物线y=ax2+bx+c的部分图象如图所示，若y＞0，则x的取值范围是-3＜x＜1．
分析 首先根据抛物线与x轴的交点关于对称轴对称求得与x轴的交点，则求y＞0时x的取值范围就是求二次函数的图象在x轴上方时对应的自变量的取值范围．
解答 解：点（1，0）关于直线x=-1的对称点是（-3，0）．
则当y＞0时，x的范围是-3＜x＜1．
故答案是：-3＜x＜1．
点评 本题考查了二次函数与不等式的关系，理解求y＞0时x的取值范围就是求二次函数的图象在x轴上方时对应的自变量的取值范围是关键．
练习册系列答案
相关题目
11．一个数的绝对值小于3，那么这个数不可能是（ ）
| A． | 0 | B． | 2 | C． | -2 | D． | -3 |
12．
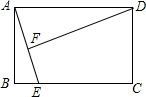如图，矩形ABCD中，AB=3，AD=4，动点E从B点沿BC边移动到C停止，DF⊥AE于F，设E在运动过程中，AE长为x，DF长为y，则下列能反映y与x函数关系的是（ ）
如图，矩形ABCD中，AB=3，AD=4，动点E从B点沿BC边移动到C停止，DF⊥AE于F，设E在运动过程中，AE长为x，DF长为y，则下列能反映y与x函数关系的是（ ）| A． | y=7x | B． | y=$\frac{12}{x}$ | C． | y=$\frac{12}{x}（3≤x≤5）$ | D． | y=$\frac{6}{x}$ |
9．下列说法正确的是（ ）
| A． | 线段AB和线段BA表示的不是同一条线段 | |
| B． | 射线AB和射线BA表示的是同一条射线 | |
| C． | 若点P是线段AB的中点，则PA=$\frac{1}{2}$AB | |
| D． | 线段AB叫做A、B两点间的距离 |
已知一次函数的图象过如图两点．
如图，已知A、B两个村庄的坐标分别为（2，3），（6，4），一辆汽车从原点O出发在x轴上行驶．
如图，抛物线y1=-$\frac{1}{2}$x2+bx+c经过点A（4，0）和B（1，0），与y轴交于点C．