题目内容
12.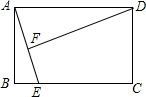 如图,矩形ABCD中,AB=3,AD=4,动点E从B点沿BC边移动到C停止,DF⊥AE于F,设E在运动过程中,AE长为x,DF长为y,则下列能反映y与x函数关系的是( )
如图,矩形ABCD中,AB=3,AD=4,动点E从B点沿BC边移动到C停止,DF⊥AE于F,设E在运动过程中,AE长为x,DF长为y,则下列能反映y与x函数关系的是( )| A. | y=7x | B. | y=$\frac{12}{x}$ | C. | y=$\frac{12}{x}(3≤x≤5)$ | D. | y=$\frac{6}{x}$ |
分析 根据题意,∠ABD=∠AFD=90°;∠AEB=∠DAF.得到△ABE与△ADF相似.运用相似三角形的性质得关系式.
解答 解:矩形ABCD中,AB=3,AD=4,DF⊥AE,
∴∠ABE=∠AFD=90°,AB=AD=4,AD∥BC.
∴∠DAF=∠AEB.
∴△ABE∽△DFA.
∴AE:AD=AB:DF,
即 x:4=3:y,
∴y=$\frac{12}{x}$.
故选C.
点评 此题考查矩形的性质,相似三角形的判定与性质,求函数的关系式,熟练掌握相似三角形的判定定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2. 我县教育局为提高教师的教学水平,在全范围举行了数学比武,其中10名参加决赛的教师的参赛成绩统计如图所示,对于这10名教师的参赛成绩,下列说法中错误的是( )
我县教育局为提高教师的教学水平,在全范围举行了数学比武,其中10名参加决赛的教师的参赛成绩统计如图所示,对于这10名教师的参赛成绩,下列说法中错误的是( )
 我县教育局为提高教师的教学水平,在全范围举行了数学比武,其中10名参加决赛的教师的参赛成绩统计如图所示,对于这10名教师的参赛成绩,下列说法中错误的是( )
我县教育局为提高教师的教学水平,在全范围举行了数学比武,其中10名参加决赛的教师的参赛成绩统计如图所示,对于这10名教师的参赛成绩,下列说法中错误的是( )| A. | 众数是90 | B. | 中位数是90 | C. | 平均数是90 | D. | 极差是15 |
20.用一个平面截正方体所得的截面图形不可能是( )
| A. | 六边形 | B. | 五边形 | C. | 菱形 | D. | 直角三角形 |
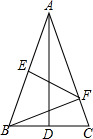 如图,△ABC,AB=AC,AD为△ABC的角平分线,过AB的中点E作AB的垂线交AC于点F,连接BF,若AB=5,CD=2,则△BFC的周长为( )
如图,△ABC,AB=AC,AD为△ABC的角平分线,过AB的中点E作AB的垂线交AC于点F,连接BF,若AB=5,CD=2,则△BFC的周长为( )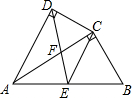 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F,AD=4,AB=6.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F,AD=4,AB=6.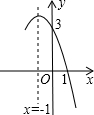 已知抛物线y=ax2+bx+c的部分图象如图所示,若y>0,则x的取值范围是-3<x<1.
已知抛物线y=ax2+bx+c的部分图象如图所示,若y>0,则x的取值范围是-3<x<1.