题目内容
6. 如图,已知A、B两个村庄的坐标分别为(2,3),(6,4),一辆汽车从原点O出发在x轴上行驶.
如图,已知A、B两个村庄的坐标分别为(2,3),(6,4),一辆汽车从原点O出发在x轴上行驶.(1)汽车行驶到什么位置时离A村最近?写出此点的坐标;
(2)汽车行驶到什么位置时离B村最近?写出此点的坐标;
(3)汽车行驶到什么位置时,距离两村的和最短?请在图中画出这个位置,并求出此时汽车到两村距离的和.
分析 (1)(2)由垂线段的性质求解即可;
(3)作点A关于x轴的对称点A′,连接A′B交x轴与点C,点C即为所求,最后依据两点间的距离公式求得A′B的距离即可.
解答 解:(1)由垂线段最短可知当汽车位于(2,0)处时,汽车距离A点最近;
(2)由垂线段最短可知当汽车位于(6,0)处时,汽车距离B点最近;
(3)如图所示:点C即为所求.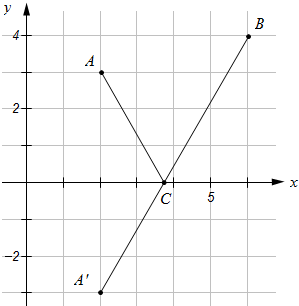
∵由轴对称的性质可知:AC=A′C,
∴AC+BC=A′C+BC=A′B=$\sqrt{(6-2)^{2}+(4+3)^{2}}$=$\sqrt{65}$.
点评 本题主要考查的是轴对称路径最短、两点间的距离公式、垂线段的性质,明确当点A′、C、B在一条直线上时点C到A、B两点的距离之和最短时解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
14.点(0,3)的位置在( )
| A. | x轴正半轴 | B. | x轴负半轴 | C. | y轴正半轴 | D. | y轴负半轴 |
11.计算(1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$)•($\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$)-(1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$-$\frac{1}{5}$)•($\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$)的结果是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
15. 如图,?ABCD的对角线交于点O,且CD=4,若它的对角线的和是32,则△AOB的周长为( )
如图,?ABCD的对角线交于点O,且CD=4,若它的对角线的和是32,则△AOB的周长为( )
 如图,?ABCD的对角线交于点O,且CD=4,若它的对角线的和是32,则△AOB的周长为( )
如图,?ABCD的对角线交于点O,且CD=4,若它的对角线的和是32,则△AOB的周长为( )| A. | 18 | B. | 20 | C. | 22 | D. | 24 |
16.我国自主研制的“天河二号”超级计算机,其浮点运算速度高达每秒33.86千万亿次.33.86千万用科学记数法表示为( )
| A. | 0.3386×109 | B. | 3.386×108 | C. | 3.386×109 | D. | 33.86×107 |
 如图,在△ABC中,AB=AD=DC,∠BAD=24°,求∠BAC的度数.
如图,在△ABC中,AB=AD=DC,∠BAD=24°,求∠BAC的度数.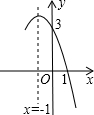 已知抛物线y=ax2+bx+c的部分图象如图所示,若y>0,则x的取值范围是-3<x<1.
已知抛物线y=ax2+bx+c的部分图象如图所示,若y>0,则x的取值范围是-3<x<1. 某地连续统计了10天日最高气温,并绘制成如图所示的扇形统计图.计算这10天日最高气温的平均值为34.3℃.
某地连续统计了10天日最高气温,并绘制成如图所示的扇形统计图.计算这10天日最高气温的平均值为34.3℃.