题目内容
10. 如图,抛物线y1=-$\frac{1}{2}$x2+bx+c经过点A(4,0)和B(1,0),与y轴交于点C.
如图,抛物线y1=-$\frac{1}{2}$x2+bx+c经过点A(4,0)和B(1,0),与y轴交于点C.(1)求出抛物线的解析式;
(2)求点C的坐标及抛物线的顶点坐标;
(3)设直线AC的解析式为y2=mx+n,请直接写出当y1<y2时,x的取值范围.
分析 (1)把A和B的坐标代入函数解析式求得b和c的值,即可求得函数解析式;
(2)在函数解析式中令x=0即可求得C的坐标,然后利用配方法即可确定顶点坐标;
(3)当y1<y2时x的范围就是当二次函数的图象在一次函数的图象的下边时对应的x的范围,依据图象即可确定.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{-\frac{1}{2}×16+4b+c=0}\\{-\frac{1}{2}+b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=\frac{5}{2}}\\{c=-2}\end{array}\right.$.
则抛物线的解析式是y=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2;
(2)在y=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2中令x=0,则y=-2,
则C的坐标是(0,-2).
y=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2=-$\frac{1}{2}$(x-$\frac{5}{2}$)2+$\frac{9}{8}$,
则抛物线的顶点坐标是($\frac{5}{2}$,$\frac{9}{8}$);
(3)当y1<y2时,x的取值范围是x<0或x>4.
点评 本题考查了待定系数法求函数的解析式,以及通过图象确定自变量的范围,考查了数形结合的思想.

练习册系列答案
相关题目
20.用一个平面截正方体所得的截面图形不可能是( )
| A. | 六边形 | B. | 五边形 | C. | 菱形 | D. | 直角三角形 |
15. 如图,?ABCD的对角线交于点O,且CD=4,若它的对角线的和是32,则△AOB的周长为( )
如图,?ABCD的对角线交于点O,且CD=4,若它的对角线的和是32,则△AOB的周长为( )
 如图,?ABCD的对角线交于点O,且CD=4,若它的对角线的和是32,则△AOB的周长为( )
如图,?ABCD的对角线交于点O,且CD=4,若它的对角线的和是32,则△AOB的周长为( )| A. | 18 | B. | 20 | C. | 22 | D. | 24 |
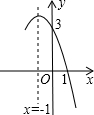 已知抛物线y=ax2+bx+c的部分图象如图所示,若y>0,则x的取值范围是-3<x<1.
已知抛物线y=ax2+bx+c的部分图象如图所示,若y>0,则x的取值范围是-3<x<1. 某地连续统计了10天日最高气温,并绘制成如图所示的扇形统计图.计算这10天日最高气温的平均值为34.3℃.
某地连续统计了10天日最高气温,并绘制成如图所示的扇形统计图.计算这10天日最高气温的平均值为34.3℃.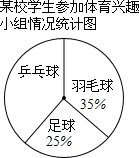 某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有40人.
某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有40人.