题目内容
12.在中央电视台第2套《购物街》栏目中,有一个精彩刺激的游戏--幸运大转盘,其规则如下:①游戏工具是一个可绕轴心自由转动的圆形转盘,转盘按圆心角均匀划分为20等分,并在其边缘标记5、10、15、…、100共20个5的整数倍数,游戏时,选手可旋转转盘,待转盘停止时,指针所指的数即为本次游戏的得分;
②每个选手在旋转一次转盘后可视得分情况选择是否再旋转转盘一次,若只旋转一次,则以该次得分为本轮游戏的得分,若旋转两次则以两次得分之和为本轮游戏的得分;
③若某选手游戏得分超过100分,则称为“爆掉”,该选手本轮游戏裁定为“输”,在得分不超过100分的情况下,分数高者裁定为“赢”;
④遇到相同得分的情况,相同得分的选手重新游戏,直到分出输赢.
现有甲、乙两位选手进行游戏,请解答以下问题:
(1)甲已旋转转盘一次,得分65分,他选择再旋转一次,求他本轮游戏不被“爆掉”的概率.
(2)若甲一轮游戏最终得分为90分,乙第一次旋转转盘得分为85分,则乙还有可能赢吗?赢的概率是多少?
(3)若甲、乙两人交替进行游戏,现各旋转一次后甲得85分,乙得65分,你认为甲是否应选择旋转第二次?说明你的理由.
分析 (1)首先根据选手两次游戏得分超过100分时被“爆掉”,求出甲第二次可取的数有多少;然后根据概率公式,求出甲本轮游戏不被“爆掉”的概率是多少即可.
(2)乙有可能赢.首先根据选手两次游戏得分超过100分时被“爆掉”,求出乙第二次可取的数有多少;然后根据概率公式,求出乙赢的概率是多少即可.
(3)甲选择不转第二次.理由是:甲选择不转第二次,乙必须选择旋转第二次,根据概率公式,求出乙获胜的可能性是多少,可得乙获胜的可能性较小.
解答 解:(1)∵选手两次游戏得分超过100分时被“爆掉”,
∴甲第二次可取5、10、15、20、25、30、35,
∴P(甲不被爆掉)=$\frac{7}{20}$.
(2)乙有可能赢.
∵选手两次游戏得分超过100分时被“爆掉”,
∴乙第二次可取5、10、15,
∴P(乙赢)=$\frac{3}{20}$.
(3)甲选择不转第二次.
理由是:甲选择不转第二次,乙必须选择旋转第二次,
∵选手两次游戏得分超过100分时被“爆掉”,
∴乙获胜的话,第二次可取25、30、35,
此时P(乙赢)=$\frac{3}{20}$,
∴乙获胜的可能性较小.
点评 此题主要考查了概率公式的应用,要熟练掌握,解答此题的关键是要明确:随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.

练习册系列答案
相关题目
17.一个自然数a的算术平方根为x,那么a+1的立方根是( )
| A. | ±$\root{3}{a+1}$ | B. | $\root{3}{{{{(x+1)}^2}}}$ | C. | $\root{3}{{{x^2}+1}}$ | D. | ±$\root{3}{{{x^2}+1}}$ |
 如图,在?ABCD中,E,F分别是BC,CD的中点,AE=3,AF=4,∠EAF=60°,则?ABCD的面积是8$\sqrt{3}$.
如图,在?ABCD中,E,F分别是BC,CD的中点,AE=3,AF=4,∠EAF=60°,则?ABCD的面积是8$\sqrt{3}$.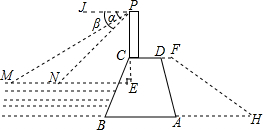
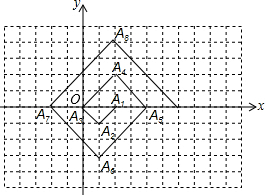 如图,在单位为1的正方形网格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2015的坐标为(-1006,0).
如图,在单位为1的正方形网格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2015的坐标为(-1006,0).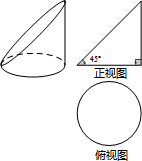 某圆柱被一平面所截得到的几何体如图所示,若该几何体的正视图是等腰直角三角形,俯视图是圆(如右图),则它的侧视图是( )
某圆柱被一平面所截得到的几何体如图所示,若该几何体的正视图是等腰直角三角形,俯视图是圆(如右图),则它的侧视图是( )