题目内容
2.已知抛物线y=-x2+2mx-4与直线y=mx+2有两个交点,且两个交点位于直线x=1的两侧,求m的取值范围m>7.分析 设抛物线y=-x2+2mx-4与直线y=mx+2有两个交点的横坐标为a和b,a>1,b<1,根据抛物线与一次函数的交点问题得到a、b为方程-x2+2mx-4=mx+2的两个解,整理得x2-mx+6=0,根据根与系数的关系得到a+b=m,ab=6,然后利用(a-1)(b-1)<0得到6-m+1<0,然后解关于m的不等式即可.
解答 解:设抛物线y=-x2+2mx-4与直线y=mx+2有两个交点的横坐标为a和b,a>1,b<1,
则a、b为方程-x2+2mx-4=mx+2的两个解,
整理得x2-mx+6=0,
a+b=m,ab=6,
而(a-1)(b-1)<0,
即ab-(a+b)+1<0,
所以6-m+1<0,
所以m>7.
故答案为m>7.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.也考查了根与系数的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
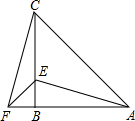 在△ABC中,∠ACB=45°,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF
在△ABC中,∠ACB=45°,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF 如图,BD是等腰Rt△ABC斜边AC上的高,AE平分∠BAC,交BC于点E,交BD于点F.求证:CE=2DF.
如图,BD是等腰Rt△ABC斜边AC上的高,AE平分∠BAC,交BC于点E,交BD于点F.求证:CE=2DF.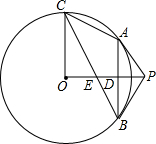 如图所示,已知P为⊙O外一点,PA为⊙O的切线,A为切点,B为⊙O上一点,且PA=PB,连接OP、AB相交于点D,过点O作OC⊥OP交⊙O于C,连接BC交OP于E.
如图所示,已知P为⊙O外一点,PA为⊙O的切线,A为切点,B为⊙O上一点,且PA=PB,连接OP、AB相交于点D,过点O作OC⊥OP交⊙O于C,连接BC交OP于E.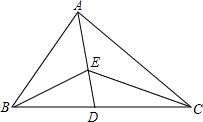 如图,AD为△ABC的角平分线,点E在AD上.
如图,AD为△ABC的角平分线,点E在AD上.