题目内容
3. 如图,在?ABCD中,E,F分别是BC,CD的中点,AE=3,AF=4,∠EAF=60°,则?ABCD的面积是8$\sqrt{3}$.
如图,在?ABCD中,E,F分别是BC,CD的中点,AE=3,AF=4,∠EAF=60°,则?ABCD的面积是8$\sqrt{3}$.
分析 延长AE,DC交于G,连接AC,过F作FH⊥AE于H,根据已知条件推出△ABE≌△GCE,得到GE=AE=3,于是得到S△AEC=S△AFC=S△GEC=$\frac{1}{4}$S四边形ABCD,求出S△AGF=×$6×2\sqrt{3}$=6$\sqrt{3}$,得到S△AEC=$\frac{1}{3}$S△AGF=2$\sqrt{3}$,即可得到结果.
解答  解:延长AE,DC交于G,连接AC,过F作FH⊥AE于H,
解:延长AE,DC交于G,连接AC,过F作FH⊥AE于H,
在?ABCD中,∵AB∥CD,
∴∠B=∠BCG,
∵E,F分别是BC,CD的中点,
∴BE=CE,
在△ABE与△GCE中,$\left\{\begin{array}{l}{∠B=∠ECG}\\{BE=CE}\\{∠AEB=∠GEC}\end{array}\right.$
∴△ABE≌△GCE,
∴GE=AE=3,
∵AF=4,∠EAF=60°,∴FH=2$\sqrt{3}$,
∴S△AEC=S△AFC=S△GEC=$\frac{1}{4}$S四边形ABCD,
∵AG=6,FH=2$\sqrt{3}$,
∴S△AGF=$\frac{1}{2}$×$6×2\sqrt{3}$=6$\sqrt{3}$,
∴S△AEC=$\frac{1}{3}$S△AGF=2$\sqrt{3}$,
∴S四边形ABCD=4S△AEC=8$\sqrt{3}$.
故答案为:8$\sqrt{3}$.
点评 本题考查了平行四边形的性质,全等三角形的判定与性质,平行四边形的面积,三角形的面积,正确的作出辅助线是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
15. 如图,AB是圆O的直径,点D在AB的延长线上,DC切圆O于C,若∠A=25°.则∠D等于( )
如图,AB是圆O的直径,点D在AB的延长线上,DC切圆O于C,若∠A=25°.则∠D等于( )
 如图,AB是圆O的直径,点D在AB的延长线上,DC切圆O于C,若∠A=25°.则∠D等于( )
如图,AB是圆O的直径,点D在AB的延长线上,DC切圆O于C,若∠A=25°.则∠D等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
13.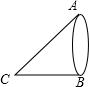 如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
 如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )
如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的C点测得CA=130米,CB=120米,则AB为( )| A. | 30米 | B. | 40米 | C. | 50米 | D. | 60米 |
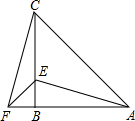 在△ABC中,∠ACB=45°,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF
在△ABC中,∠ACB=45°,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF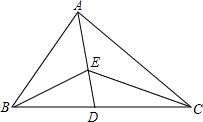 如图,AD为△ABC的角平分线,点E在AD上.
如图,AD为△ABC的角平分线,点E在AD上.