题目内容
15.己知抛物线y=ax2+c的图象与x轴交于A、B两点,与y轴交于C点.若△ABC的面积等于4$\sqrt{3}$,则它的解析式为( )| A. | y=$\sqrt{3}$x2-3$\sqrt{3}$ | B. | y=-2$\sqrt{3}{x}^{2}+2\sqrt{3}$ | C. | y=$\sqrt{3}{x}^{2}$-4$\sqrt{3}$ | D. | y=-$\frac{\sqrt{3}}{2}{x}^{2}+2\sqrt{3}$ |
分析 令x=0求得抛物线与x轴的交点坐标,得到AB的长,令x=0求得C坐标,然后再求得三角形ABC的面积即可做出判断.
解答 解:A、令x=0得:y=-3$\sqrt{3}$,令y=0得$\sqrt{3}$x2-3$\sqrt{3}$=0,解得:${x}_{1}=\sqrt{3}$,${x}_{2}=-\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}×2\sqrt{3}×3\sqrt{3}$=9,与原题不符,故A错误;
B、令x=0得:y=2$\sqrt{3}$,令y=0得-2$\sqrt{3}$x2+2$\sqrt{3}$=0,解得:x1=1,x2=-1,
∴△ABC的面积=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,与原题不符,故B错误;
C、令x=0得:y=-4$\sqrt{3}$,令y=0得$\sqrt{3}$x2-4$\sqrt{3}$=0,解得:x1=2,x2=-2,
∴△ABC的面积═$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$,与原题不符,故C错误;
D、令x=0得:y=2$\sqrt{3}$,令y=0得$-\frac{\sqrt{3}}{2}$x2+2$\sqrt{3}$=0,解得:x1=2,x2=-2,
∴△ABC的面积=$\frac{1}{2}×4×2\sqrt{3}$=4$\sqrt{3}$,故D正确.
故选:D.
点评 本题主要考查的是抛物线与坐标轴的交点,掌握抛物线与两坐标交点坐标的求法是解题的关键.

练习册系列答案
相关题目
6.下列计算正确的是( )
| A. | 6÷3×$\frac{1}{3}$=6 | B. | $\frac{1}{2}$-$\frac{1}{2}$×3=0 | C. | -32-(-23)=1 | D. | (-1$\frac{1}{2}$)2=$\frac{9}{4}$ |
20.下列方程中,关于x的一元二次方程是( )
| A. | x2+x+y=0 | B. | $\frac{1}{2}$x2-3x+1=0 | C. | (x+3)2=x2+2x | D. | ${x^2}+\frac{1}{x}=2$ |
7.下列各式正确的是( )
| A. | (a+b)2=a2+b2 | B. | (a+b)(b-a)=b2-a2 | C. | (a-b)2=a2-2ab-b2 | D. | (-a+3)2=-a2-6a+9 |
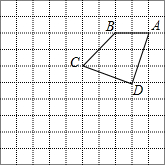 如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.
如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.