题目内容
5.若抛物线y=$\frac{1}{2}$x2-mx+5m2与x轴有交点,则m的取值范围为m=0.分析 抛物线y=$\frac{1}{2}$x2-mx+5m2与x轴有交点,则△=b2-4ac≥0,从而求出m的取值范围即可.
解答 解:∵y=$\frac{1}{2}$x2-mx+5m2与x轴有交点,
∴方程$\frac{1}{2}$x2-mx+5m2=0与x轴有交点,
∴△=b2-4ac=m2-4×$\frac{1}{2}$×5m2≥0,
∴-9m2≥0,
∴m=0.
故答案为m=0.
点评 本题考查了抛物线与x轴的交点问题,注:①抛物线与x轴有两个交点,则△>0;②抛物线与x轴无交点,则△<0;③抛物线与x轴有一个交点,则△=0.

练习册系列答案
相关题目
15.己知抛物线y=ax2+c的图象与x轴交于A、B两点,与y轴交于C点.若△ABC的面积等于4$\sqrt{3}$,则它的解析式为( )
| A. | y=$\sqrt{3}$x2-3$\sqrt{3}$ | B. | y=-2$\sqrt{3}{x}^{2}+2\sqrt{3}$ | C. | y=$\sqrt{3}{x}^{2}$-4$\sqrt{3}$ | D. | y=-$\frac{\sqrt{3}}{2}{x}^{2}+2\sqrt{3}$ |
10.-|-$\frac{1}{2}$|的相反数的倒数是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
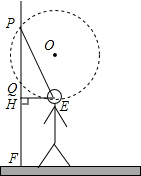 如图,墙壁上的展品最高点与地面的距离PF=3.2m,最低点与地面的距离QF=2m,观赏者的眼睛E距地面1.6m,经验表明,当水平视线EH与过P,Q,E点的圆相切于点E时,视角最大,站在此处观赏最理想,求此时点E到墙壁的距离EH.
如图,墙壁上的展品最高点与地面的距离PF=3.2m,最低点与地面的距离QF=2m,观赏者的眼睛E距地面1.6m,经验表明,当水平视线EH与过P,Q,E点的圆相切于点E时,视角最大,站在此处观赏最理想,求此时点E到墙壁的距离EH. 王华的爷爷开发了一块四边形菜地,测量数据如图所示,请你计算此块地的面积.
王华的爷爷开发了一块四边形菜地,测量数据如图所示,请你计算此块地的面积.