题目内容
19. 已知抛物线的解析式为:y=x2-4x+3在平面直角坐标系中画出这条抛物线.
已知抛物线的解析式为:y=x2-4x+3在平面直角坐标系中画出这条抛物线.(1)求这条抛物线与x轴的交点坐标.
(2)结合图象说明x取何值时y>0.
(3)当x取何值时,y随x的增大而减小?
分析 利用列表、描点、连线即可画出这条抛物线.
(1)在解析式中令y=0即可求得与x轴的交点的横坐标;
(2)(3)根据图象即可解答.
解答 解:列表:
 ;
;
(1)在y=x2-4x+3中,令y=0,则x2-4x+3=0,
解得:x1=1,x2=3,
则抛物线与x轴的交点坐标是(1,0)和(3,0);
(2)当x<1或x>3时,y>0;
(3)当x<2时,y随x的增大而减小.
点评 此题考查了二次函数的图象的作法以及二次函数的性质,正确作出函数的图象,理解函数的增减性是解决问题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
4. 如图,直线l1与l2相交,且夹角为60°,点P在角的内部,小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,…,如此继续,得到一系列的点P1,P2,…,Pn,若Pn与P重合,则n的可以是( )
如图,直线l1与l2相交,且夹角为60°,点P在角的内部,小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,…,如此继续,得到一系列的点P1,P2,…,Pn,若Pn与P重合,则n的可以是( )
 如图,直线l1与l2相交,且夹角为60°,点P在角的内部,小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,…,如此继续,得到一系列的点P1,P2,…,Pn,若Pn与P重合,则n的可以是( )
如图,直线l1与l2相交,且夹角为60°,点P在角的内部,小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,…,如此继续,得到一系列的点P1,P2,…,Pn,若Pn与P重合,则n的可以是( )| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2012 |
9.已知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点M(-2,2),则k的值是( )
| A. | -4 | B. | -1 | C. | 1 | D. | 4 |
 如图,直线y=kx+b经过A(1,-1)、B(-1,3),则-1<kx+b<3的解集为-1<x<1.
如图,直线y=kx+b经过A(1,-1)、B(-1,3),则-1<kx+b<3的解集为-1<x<1.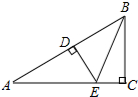 如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=3cm.
如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=3cm.
 如图,在Rt△OAB中,∠OAB=90°,点B的坐标为(4,2).
如图,在Rt△OAB中,∠OAB=90°,点B的坐标为(4,2).