题目内容
2．
如图：△ABC中，AD为∠BAC的角平分线，EF垂直平分AD，E为垂足，EF交BC的延长线于点F，求证：∠B=∠CAF．
分析 EF垂直平分AD，则可得AF=DF，进而再转化为角之间的关系，通过角之间的平衡转化，最终得出结论．
解答 证明：∵EF垂直平分AD，
∴AF=DF，
∴∠ADF=∠DAF，
∵∠ADF=∠B+∠BAD，
∠DAF=∠CAF+∠CAD，
又∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴∠B=∠CAF．
点评 此题主要考查线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段的两个端点的距离相等．
练习册系列答案
相关题目
如图，直线y=kx+b经过A（1，-1）、B（-1，3），则-1＜kx+b＜3的解集为-1＜x＜1．
17．
如图中，如图的几何体展开图是（ ）
如图中，如图的几何体展开图是（ ）| A． |  | B． |  | C． |  | D． |  |
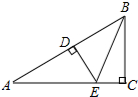如图：∠C=90°，DE⊥AB，垂足为D，BC=BD，若AC=3cm，则AE+DE=3cm．
如图，在Rt△OAB中，∠OAB=90°，点B的坐标为（4，2）．