题目内容
14.观察下面的变形规律:$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1,$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}-\sqrt{2}$,$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\sqrt{4}-\sqrt{3}$,$\frac{1}{\sqrt{5}+\sqrt{4}}$=$\sqrt{5}-\sqrt{4}$…
解答下面的问题:
(1)若n为正整数,请你猜想$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$.
(2)计算($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2012}}$)×($\sqrt{2013}$+1)
分析 (1)直接利用分母有理化法则化简求出答案;
(2)直接利用分母有理化法则化简,再利用平方差公式求出答案.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$.
故答案为:$\sqrt{n+1}$-$\sqrt{n}$;
(2)($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2012}}$)×($\sqrt{2013}$+1)
=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2013}$-$\sqrt{2012}$)($\sqrt{2013}$+1)
=($\sqrt{2013}$-1)($\sqrt{2013}$+1)
=2012.
点评 此题主要考查了分母有理化,正确化简二次根式是解题关键.

练习册系列答案
相关题目
4.下列叙述错误的是( )
| A. | 单项式x2y的系数是1 | B. | -x4y3、0、$\frac{x}{3}$都是单项式 | ||
| C. | 3a2-5ab+b4-5是四次四项式 | D. | 多项式与多项式的和一定是多项式 |
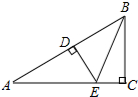 如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=3cm.
如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=3cm.