题目内容
15.已知a2-3a+1=0,求$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}+5}$的值.分析 让等式两边同时除以a,得到a+$\frac{1}{a}$=3,两边平方整理即可得到a2+$\frac{1}{{a}^{2}}$=7的值,再代入$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}+5}$求值即可.
解答 解:∵a2-3a+1=0,
∴a-3+$\frac{1}{a}$=0,
∴a+$\frac{1}{a}$=3,
∴(a+$\frac{1}{a}$)2=9,
∴a2+$\frac{1}{{a}^{2}}$+2=9,
∴a2+$\frac{1}{{a}^{2}}$=7,
∴$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}+5}$=$\sqrt{7+5}$=2$\sqrt{3}$.
点评 此题主要考查了二次根式的求值,以及完全平方公式的应用,关键是掌握整体的数学思想的应用.

练习册系列答案
相关题目
3.小莉的密码日记本的密码是四位数,由于她忘记了密码的末位数字,则小莉能一次打开日记本的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
 如图,直线y=kx+b经过A(1,-1)、B(-1,3),则-1<kx+b<3的解集为-1<x<1.
如图,直线y=kx+b经过A(1,-1)、B(-1,3),则-1<kx+b<3的解集为-1<x<1.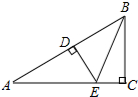 如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=3cm.
如图:∠C=90°,DE⊥AB,垂足为D,BC=BD,若AC=3cm,则AE+DE=3cm.